Study Notes
Overview
Forces and their interactions form the foundation of mechanics in GCSE Physics. This topic explores how forces cause changes in motion, how multiple forces combine to produce a resultant effect, and how objects behave under different force conditions. You will learn to apply Newton's three laws of motion, calculate forces and accelerations using F = ma, investigate the behaviour of springs using Hooke's Law, and explain phenomena such as terminal velocity. Understanding forces is critical not only for this topic but also for later topics involving energy, momentum, and motion. Exam questions in this area typically involve calculations requiring clear substitution and unit conversion, explanations of motion using the concept of resultant force, and analysis of experimental data from required practicals. You will encounter a mix of AO1 recall questions, AO2 application questions, and AO3 data analysis questions, so a well-rounded understanding is essential. This topic connects directly to energy transfers, motion graphs, and momentum, making it a synoptic hub within the specification.
Key Concepts
Concept 1: Newton's First Law (Law of Inertia)
Newton's First Law states that an object will remain at rest or continue to move at a constant velocity unless acted upon by a resultant force. This law introduces the concept of inertia, which is the tendency of an object to resist changes in its state of motion. The key term here is resultant force. If all forces acting on an object are balanced, the resultant force is zero, and there is no change in motion. For example, a book resting on a table experiences a downward force due to gravity (its weight) and an upward force from the table (the normal reaction force). These forces are equal in magnitude and opposite in direction, so the resultant force is zero, and the book remains at rest. Similarly, a car travelling at a constant speed on a straight road has balanced forces: the driving force equals the resistive forces (friction and air resistance), resulting in zero acceleration. It is crucial to understand that balanced forces do not mean no forces are acting; rather, they mean the forces cancel each other out. Candidates often lose marks by failing to refer explicitly to the resultant force when explaining motion.
Example: A cyclist travels at a steady speed of 8 m/s along a flat road. Explain why the cyclist is not accelerating. Answer: The cyclist is not accelerating because the resultant force acting on them is zero. The forward driving force from pedalling is balanced by the backward resistive forces (friction and air resistance), so there is no net force to cause a change in velocity.
Concept 2: Newton's Second Law (F = ma)
Newton's Second Law provides the quantitative relationship between force, mass, and acceleration. It states that the acceleration of an object is directly proportional to the resultant force acting on it and inversely proportional to its mass. The equation is F = ma, where F is the resultant force in Newtons (N), m is the mass in kilograms (kg), and a is the acceleration in metres per second squared (m/s²). This equation is the workhorse of forces calculations. A larger resultant force produces a greater acceleration, while a larger mass produces a smaller acceleration for the same force. When using this equation, always ensure that you show your substitution clearly before calculating the final answer. This demonstrates your method and secures marks even if your arithmetic is slightly incorrect. Remember to convert units where necessary: mass must be in kilograms (not grams), and acceleration must be in m/s² (not cm/s²). The equation can be rearranged to find any of the three variables: a = F/m or m = F/a.
Example: A car of mass 1500 kg accelerates from rest under a resultant force of 3000 N. Calculate the acceleration of the car. Solution: Write the equation: F = ma. Rearrange for a: a = F/m. Substitute: a = 3000 / 1500. Calculate: a = 2 m/s². Always include units in your final answer.
Concept 3: Newton's Third Law (Action and Reaction)
Newton's Third Law states that for every action, there is an equal and opposite reaction. This means that when object A exerts a force on object B, object B exerts an equal force in the opposite direction on object A. These forces are called action-reaction pairs. The critical detail that examiners test is that these forces act on different objects, not the same object. For example, when you push against a wall, you exert a force on the wall (the action), and the wall exerts an equal and opposite force on you (the reaction). These forces are equal in magnitude, opposite in direction, and act on different bodies. This is fundamentally different from balanced forces, which act on the same object and result in no net motion. A common mistake is to confuse Newton's Third Law pairs with balanced forces. For instance, the weight of a book and the normal reaction force from a table are not action-reaction pairs; they are balanced forces acting on the same object (the book). True action-reaction pairs involve two different objects interacting with each other.
Example: Two ice skaters, A and B, push against each other. Skater A has a mass of 50 kg and skater B has a mass of 70 kg. Explain the forces involved and predict which skater will accelerate more. Answer: When the skaters push against each other, skater A exerts a force on skater B (action), and skater B exerts an equal and opposite force on skater A (reaction). These forces are equal in magnitude but act on different skaters. Because skater A has a smaller mass, they will experience a greater acceleration (using F = ma, a = F/m). Skater A will accelerate more than skater B.
Concept 4: Hooke's Law and Springs
Hooke's Law describes the behaviour of springs when they are stretched or compressed. It states that the force needed to extend or compress a spring is directly proportional to the extension or compression, provided the elastic limit is not exceeded. The equation is F = ke, where F is the force in Newtons (N), k is the spring constant in Newtons per metre (N/m), and e is the extension in metres (m). The spring constant k is a measure of the stiffness of the spring: a higher value of k means a stiffer spring that requires more force to extend by the same amount. The elastic limit is the point beyond which the spring will not return to its original length when the force is removed. Beyond this point, the spring undergoes plastic deformation. In exam questions, you are often asked to determine the spring constant from a force-extension graph. The spring constant is the gradient of the linear section of the graph, calculated as k = ΔF / Δe (rise over run). Always ensure that extension is measured in metres, not centimetres, before substituting into the equation. This is one of the most common sources of error.
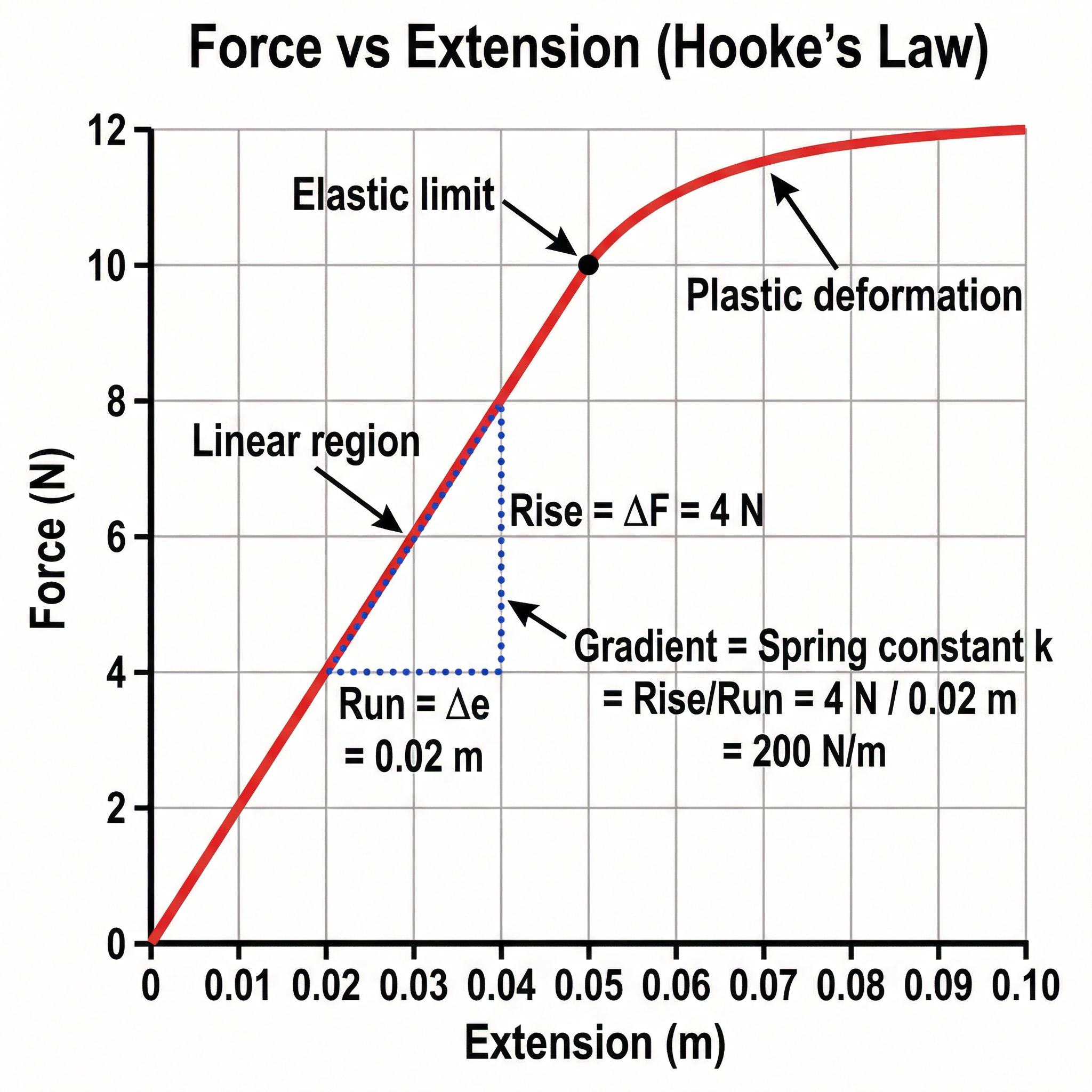
Example: A spring extends by 5 cm when a force of 10 N is applied. Calculate the spring constant. Solution: First, convert extension to metres: e = 5 cm = 0.05 m. Write the equation: F = ke. Rearrange for k: k = F/e. Substitute: k = 10 / 0.05. Calculate: k = 200 N/m.
Concept 5: Terminal Velocity
Terminal velocity is the constant maximum velocity reached by a falling object when the upward resistive force (drag or air resistance) equals the downward force due to gravity (weight). At this point, the resultant force is zero, and the object stops accelerating. Consider a skydiver jumping from a plane. Initially, the only significant force is the weight of the skydiver, pulling them downwards, so they accelerate downwards. As their speed increases, the upward drag force increases (because drag depends on velocity). Eventually, the drag force becomes equal to the weight, the resultant force becomes zero, and the skydiver falls at a constant velocity—this is terminal velocity. If the skydiver opens a parachute, the drag force suddenly increases, becoming greater than the weight. This produces an upward resultant force, causing the skydiver to decelerate. As the speed decreases, the drag force decreases until it again equals the weight, and a new, lower terminal velocity is reached. Exam questions often ask you to explain changes in motion using a velocity-time graph, so you must be able to link the shape of the graph to the forces acting.
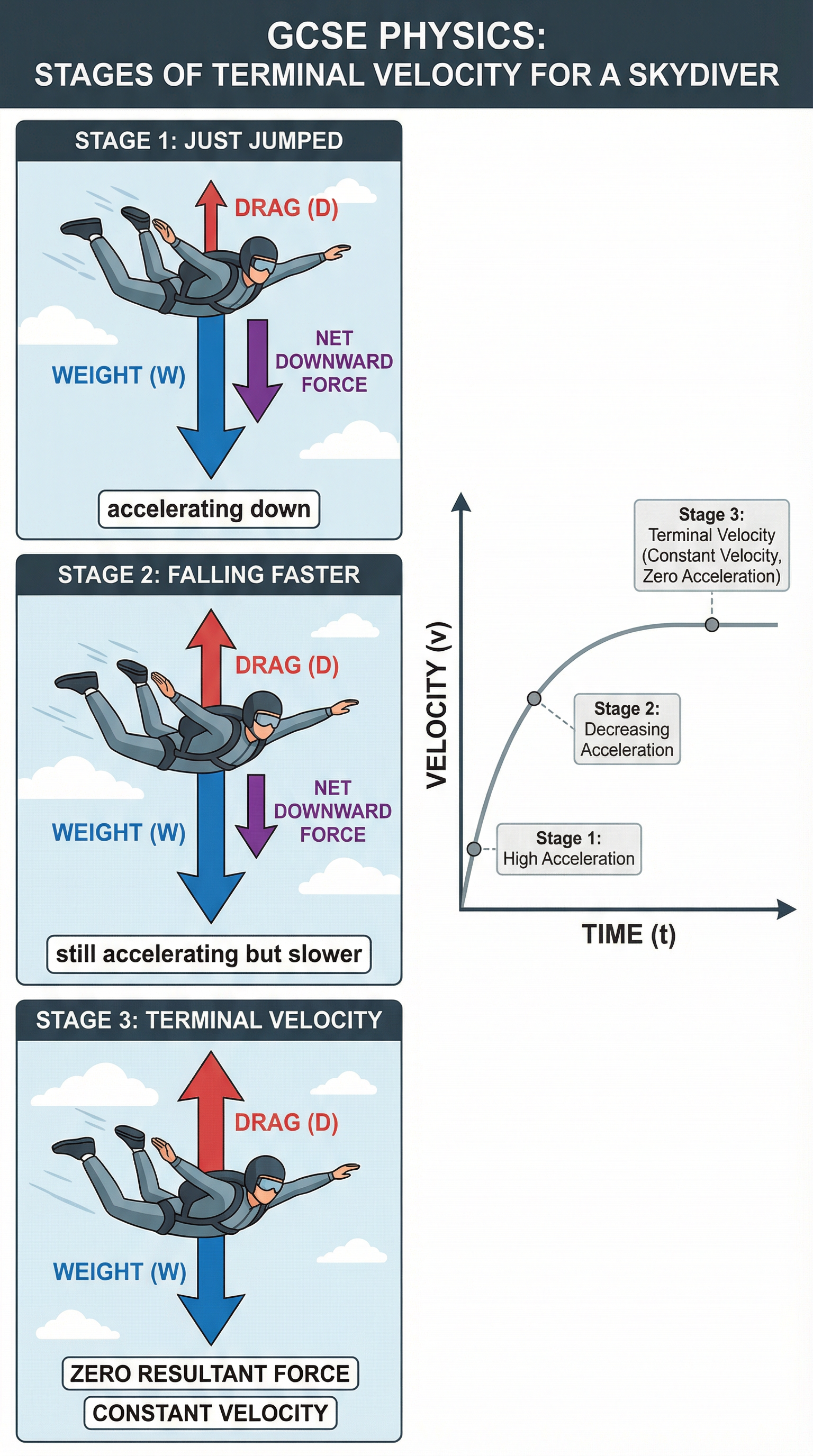
Example: A skydiver of weight 800 N reaches a terminal velocity of 50 m/s. Explain why the skydiver reaches terminal velocity. Answer: As the skydiver falls, their velocity increases, and so does the upward drag force. Eventually, the drag force becomes equal to the weight (800 N). At this point, the resultant force is zero, so the skydiver stops accelerating and falls at a constant velocity of 50 m/s.
Concept 6: Resultant Forces and Free Body Diagrams
When multiple forces act on an object, the resultant force is the single force that has the same effect as all the individual forces combined. To find the resultant force, you must consider both the magnitude and direction of each force. Forces in the same direction are added together; forces in opposite directions are subtracted. A free body diagram is a simplified diagram showing all the forces acting on an object, represented by arrows. The length of each arrow should be proportional to the magnitude of the force, and each arrow should be clearly labelled with the force name and value. Free body diagrams are essential for visualising and analysing force problems. When drawing or interpreting these diagrams, always ensure that forces are correctly labelled and that their directions are clear. Examiners will penalise vague or unlabelled diagrams.
Example: A box is pushed along a horizontal surface with a force of 50 N to the right. Friction opposes the motion with a force of 20 N to the left. Calculate the resultant force. Solution: Resultant force = 50 N (right) - 20 N (left) = 30 N to the right.
Mathematical/Scientific Relationships
Newton's Second Law: F = ma
- F = resultant force (Newtons, N)
- m = mass (kilograms, kg)
- a = acceleration (metres per second squared, m/s²)
- Must memorise
Hooke's Law: F = ke
- F = force (Newtons, N)
- k = spring constant (Newtons per metre, N/m)
- e = extension (metres, m)
- Must memorise
Weight: W = mg
- W = weight (Newtons, N)
- m = mass (kilograms, kg)
- g = gravitational field strength (Newtons per kilogram, N/kg; on Earth, g ≈ 9.8 N/kg or 10 N/kg for calculations)
- Must memorise
Rearrangements:
- From F = ma: a = F/m, m = F/a
- From F = ke: k = F/e, e = F/k
- From W = mg: m = W/g, g = W/m
Practical Applications
This topic includes a required practical investigation: Investigating the relationship between force and extension for a spring. You must be familiar with the method, expected results, and how to analyse the data.
Apparatus: Spring, clamp stand, masses (typically 100 g), metre rule or ruler, mass hanger.
Method:
- Clamp the spring vertically and attach a mass hanger to the bottom.
- Measure the initial length of the spring with no added mass.
- Add a known mass (e.g., 100 g) to the hanger and measure the new length of the spring.
- Calculate the extension (new length - original length).
- Repeat with increasing masses, recording force (F = mg) and extension each time.
- Plot a graph of force (y-axis) against extension (x-axis).
Expected Results: The graph should show a linear relationship (straight line through the origin) in the elastic region, confirming Hooke's Law. Beyond the elastic limit, the graph will curve, indicating plastic deformation.
Common Errors:
- Failing to convert mass from grams to kilograms when calculating force.
- Measuring total length instead of extension.
- Not ensuring the spring is vertical, leading to inaccurate measurements.
- Exceeding the elastic limit and damaging the spring.
How Examiners Test It: You may be given a set of results and asked to plot a graph, calculate the spring constant from the gradient, or identify the elastic limit. You might also be asked to evaluate the method or suggest improvements.
Podcast Episode
Listen to this 10-minute podcast episode for a comprehensive audio walkthrough of the key concepts, exam tips, and quick-fire recall questions. Perfect for revision on the go!
