Study Notes

Overview
Data Representation is a fundamental concept in computer science, forming the bedrock of how digital systems process and store information. At its core, this topic explores the translation of real-world data, such as numbers, text, images, and sounds, into the binary language of computers. For the OCR GCSE Computer Science exam (specification reference 2.6), a thorough understanding of data representation is not just recommended; it is essential for success. This topic is heavily weighted in assessment, with questions appearing on both Foundation and Higher tier papers, often requiring precise mathematical application and clear, justified explanations. Candidates who excel in this area can confidently tackle a significant portion of the exam, securing valuable marks through methodical application of conversion techniques and formulas. This guide will equip you with the knowledge and skills to master data representation, from the foundational principles of binary and hexadecimal systems to the practical applications of image and sound digitization. We will explore how these concepts interlink with other areas of the specification, such as computer architecture and network communication, providing a holistic understanding that is rewarded by examiners.
Key Concepts
Concept 1: Number Systems
At the heart of data representation lie the different number systems used to quantify and manipulate data. While we use the denary (base-10) system in our daily lives, computers operate on the binary (base-2) system. This is because the internal circuitry of a computer is made up of billions of transistors, which are tiny switches that can be in one of two states: on or off. These two states are represented by the binary digits 1 (on) and 0 (off), also known as bits. To make long strings of binary more manageable for human programmers, the hexadecimal (base-16) system is often used. Hexadecimal uses the digits 0-9 and the letters A-F to represent the values 0-15. The key advantage of hexadecimal is that it provides a more compact and human-readable representation of binary data, as each hexadecimal digit corresponds to a unique 4-bit binary sequence (a nibble).
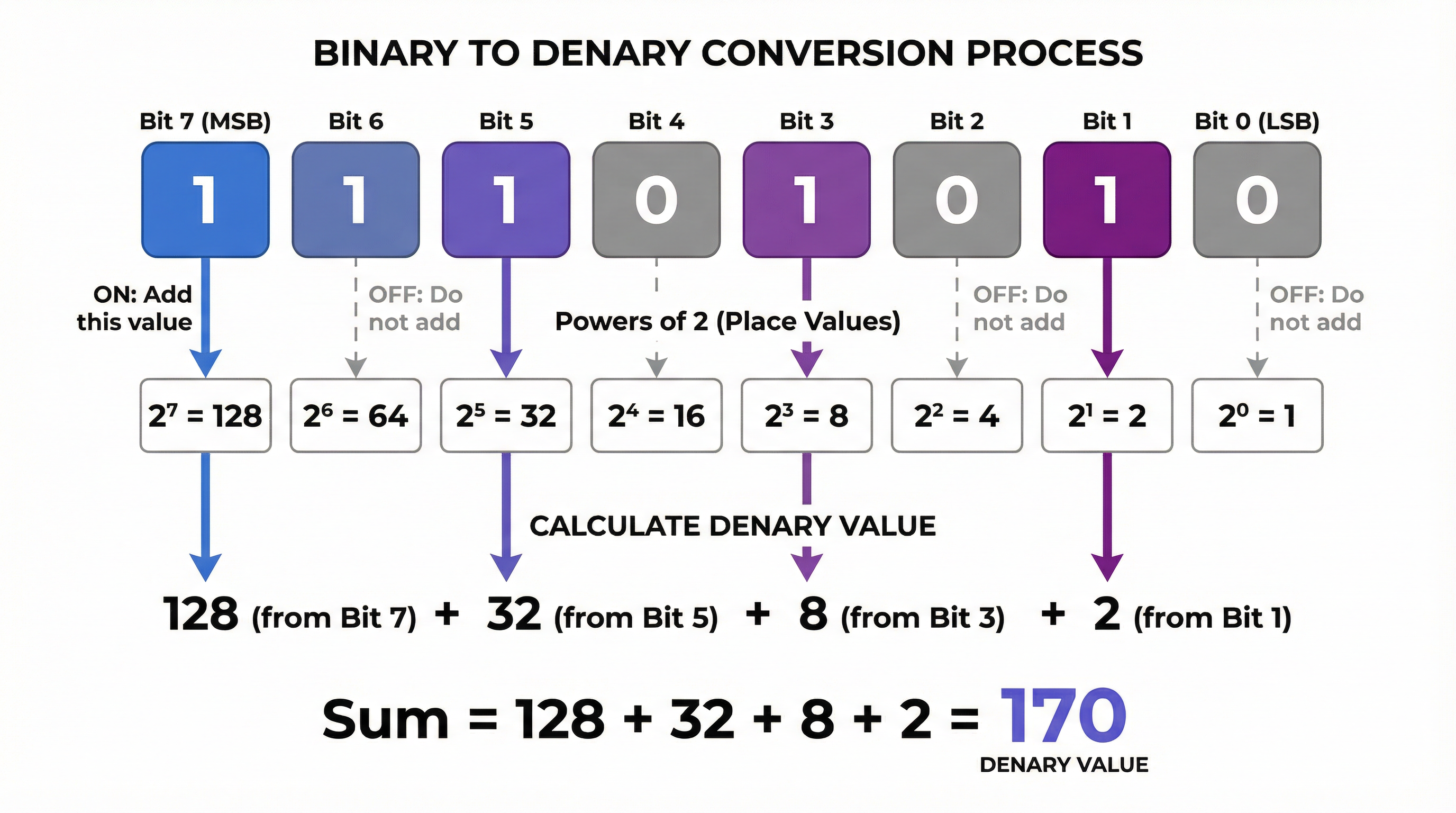
Example: The denary number 170 is represented as 10101010 in 8-bit binary, and as AA in hexadecimal.
Concept 2: Binary Arithmetic and Logical Shifts
Beyond simply representing numbers, computers must be able to perform calculations with them. Binary arithmetic involves the addition of binary numbers, following a simple set of rules. When adding two bits, 0+0=0, 0+1=1, 1+0=1, and 1+1=0 with a carry of 1 to the next column. If the result of a calculation exceeds the number of bits available to store it, an overflow error occurs. This is a critical concept, as it can lead to unexpected and incorrect results in programs. Logical shifts are operations that move the bits in a binary number to the left or right. A logical left shift multiplies a binary number by 2 for each place shifted, while a logical right shift divides it by 2. These operations are fundamental to low-level programming and are used in a variety of applications, from simple multiplication and division to complex graphical manipulations.
Concept 3: Representing Images
Digital images are composed of a grid of tiny dots called pixels. The number of pixels in an image determines its resolution, which is typically expressed as width x height (e.g., 1920x1080). The colour of each pixel is represented by a binary code, and the number of bits used to store the colour of each pixel is known as the colour depth. A higher colour depth allows for a greater number of colours to be represented, resulting in a more realistic image. For example, a 1-bit colour depth can only represent two colours (e.g., black and white), while a 24-bit colour depth can represent over 16.7 million colours. The file size of an image is determined by its resolution and colour depth, and can be calculated using the formula: Image File Size (bits) = Width (pixels) x Height (pixels) x Colour Depth (bits).
Concept 4: Representing Sound
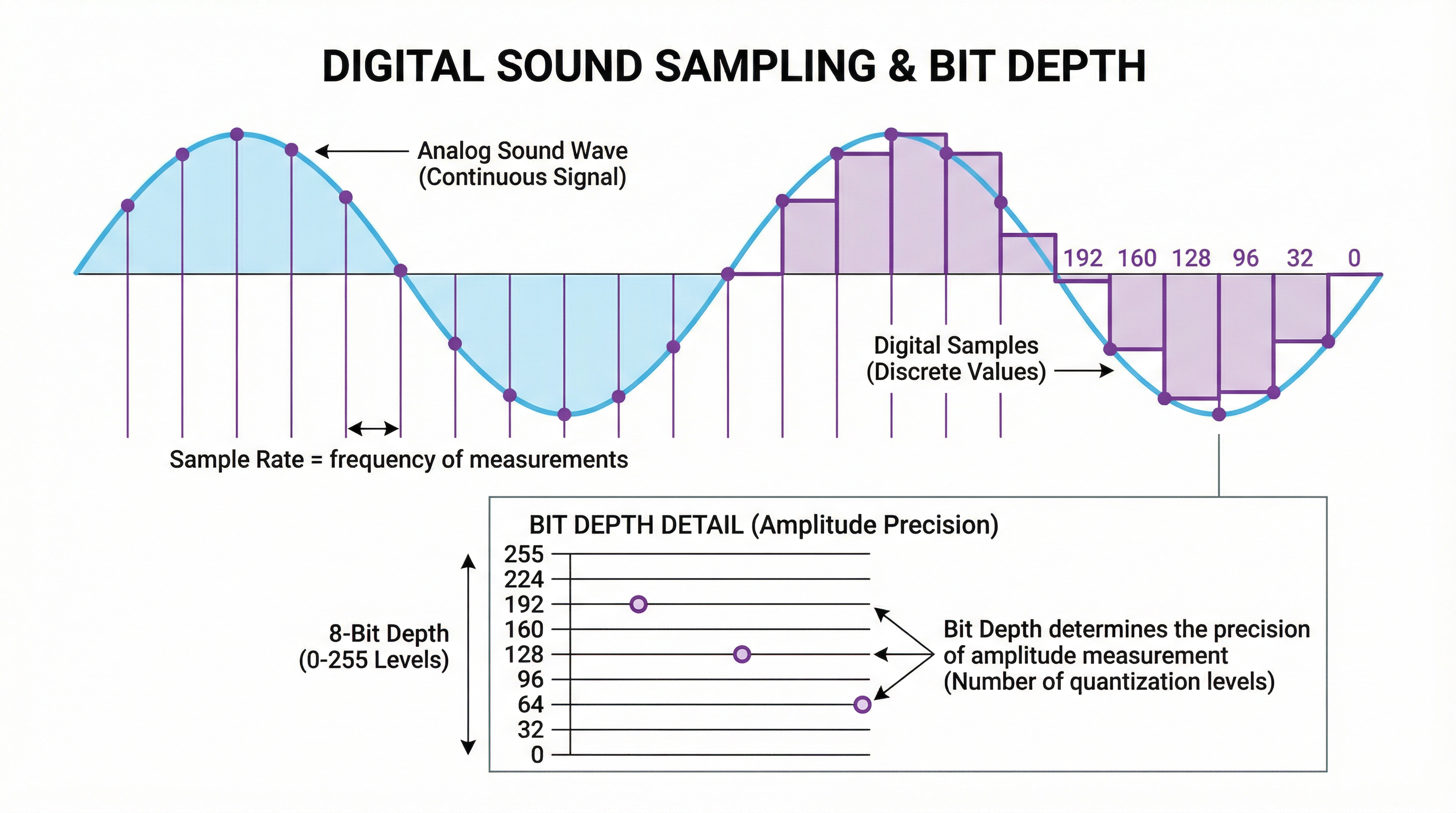
Sound is an analogue signal, meaning it is a continuous wave. To be stored and processed by a computer, it must be converted into a digital format through a process called sampling. This involves taking measurements of the sound wave's amplitude at regular intervals. The number of samples taken per second is known as the sample rate, and is measured in Hertz (Hz). A higher sample rate results in a more accurate representation of the original sound wave, and therefore higher quality audio. The bit depth determines the number of bits used to store each sample, and therefore the precision with which the amplitude of the sound wave can be represented. The file size of a sound file can be calculated using the formula: Sound File Size (bits) = Sample Rate (Hz) x Bit Depth (bits) x Duration (seconds).
Concept 5: Data Compression
Image and sound files can be very large, so they are often compressed to reduce their file size. There are two main types of compression: lossy and lossless. Lossy compression reduces file size by permanently removing some of the data from the file. This can result in a loss of quality, but is often acceptable for images and sound, where the loss may not be perceptible to the human eye or ear. JPEG and MP3 are common examples of lossy compression formats. Lossless compression, on the other hand, reduces file size without losing any data. This is achieved by identifying and eliminating redundancy in the data. When the file is uncompressed, it is restored to its original state with no loss of quality. PNG and FLAC are common examples of lossless compression formats. The choice of compression method depends on the specific requirements of the application, balancing the need for small file sizes with the importance of maintaining data integrity.
Mathematical/Scientific Relationships
- Binary to Denary Conversion: To convert an 8-bit binary number to denary, you can use the following formula, where b_n is the bit at position n (from right to left, starting at 0):
Denary = (b_7 * 2^7) + (b_6 * 2^6) + (b_5 * 2^5) + (b_4 * 2^4) + (b_3 * 2^3) + (b_2 * 2^2) + (b_1 * 2^1) + (b_0 * 2^0) - Image File Size:
Image File Size (bits) = Width (pixels) x Height (pixels) x Colour Depth (bits)(Must memorise) - Sound File Size:
Sound File Size (bits) = Sample Rate (Hz) x Bit Depth (bits) x Duration (seconds)(Must memorise) - Unit Conversions:
- 8 bits = 1 byte
- 1024 bytes = 1 kilobyte (KB)
- 1024 kilobytes = 1 megabyte (MB)
- 1024 megabytes = 1 gigabyte (GB)
Practical Applications
Data representation is not just a theoretical concept; it has numerous practical applications in the real world. Every time you view an image on a screen, listen to a song on your phone, or even type a message, you are interacting with data that has been represented in a digital format. For example, the colours you see on your screen are created by mixing different amounts of red, green, and blue light, with the intensity of each colour being represented by a binary number. The music you listen to is a digital representation of a sound wave, created by sampling the wave thousands of times per second. Understanding data representation is therefore essential for anyone who wants to work with digital media, from web designers and software developers to audio engineers and graphic artists.