Study Notes

Overview
Volume is a cornerstone of the Geometry and Measures section of your GCSE, testing your ability to apply formulas to 3D shapes. It's a topic that guarantees marks for students who are well-prepared. This guide will walk you through the essential formulas you must memorise, how to use the ones provided in your exam, and how to tackle the multi-step problems that examiners love to set. We'll cover everything from basic cylinders to complex composite shapes, ensuring you're ready for any question the exam throws at you. Understanding volume is not just about plugging numbers into a formula; it's about spatial awareness and problem-solving, skills that are highly valued. Questions often link volume to other topics like density, algebra, and unit conversions, making it a fantastic area to demonstrate synoptic understanding.
Key Concepts
Concept 1: Volume of Prisms and Cylinders
A prism is a 3D shape with a uniform cross-section. Imagine slicing a loaf of bread; every slice has the same shape. To find the volume of any prism, you use one simple rule: Volume = Area of cross-section × length. This is a formula you must memorise. A cylinder is just a special type of prism with a circular cross-section. Therefore, its volume formula is a specific version of the prism rule: Volume = πr²h (since the area of the circular cross-section is πr²). This is the second formula you must memorise.
Example: A cylinder has a radius of 5 cm and a height of 10 cm. Its volume is π × 5² × 10 = 250π cm³.
Concept 2: Volume of Pyramids, Cones, and Spheres (Higher Tier)
These shapes are more complex, but the good news is their formulas are given on the exam formula sheet. Your job is to substitute the correct values and calculate accurately.
- Cone: V = 1/3 πr²h. Notice it's 1/3 of a cylinder with the same base and height. A common error is to forget the 1/3.
- Pyramid: V = 1/3 × base area × height. This is a general form. For a square-based pyramid, the base area is simply length × width.
- Sphere: V = 4/3 πr³. Be careful to cube the radius, not square it!
Concept 3: Composite Solids
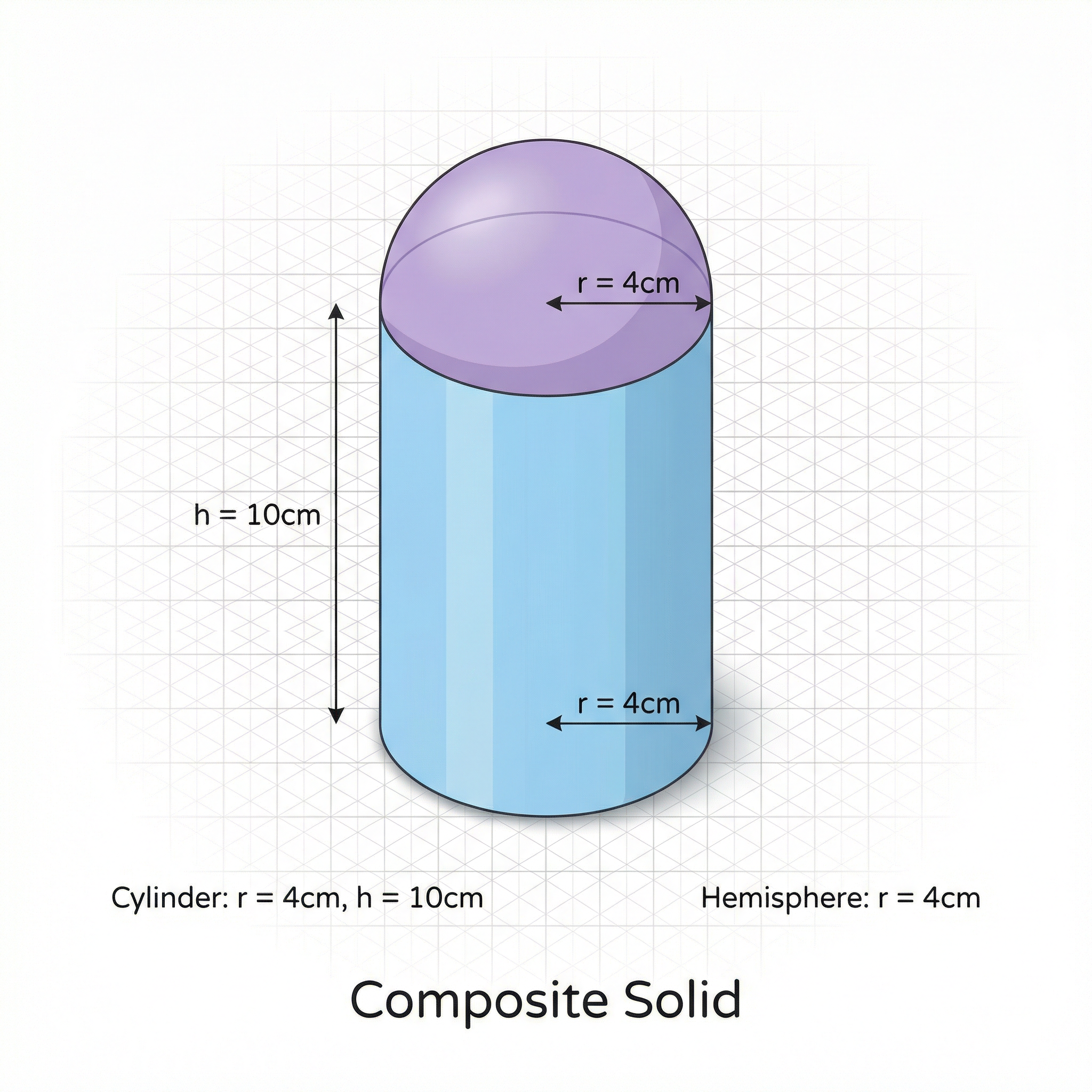
Examiners frequently ask for the volume of composite solids – shapes made from two or more simpler shapes combined. For example, a cylinder with a hemisphere on top. The strategy is to break the shape down into its components, calculate the volume of each part separately, and then add them together. Showing your working for each individual volume is crucial for securing method marks.
Concept 4: Frustums (Higher Tier)
A frustum is the shape left over when you slice the top off a cone or pyramid. To find its volume, you must:
- Calculate the volume of the original, large cone/pyramid.
- Calculate the volume of the smaller cone/pyramid that was removed.
- Subtract the small volume from the large volume. This often involves using similar triangles to find the dimensions of the removed cone.
Mathematical/Scientific Relationships
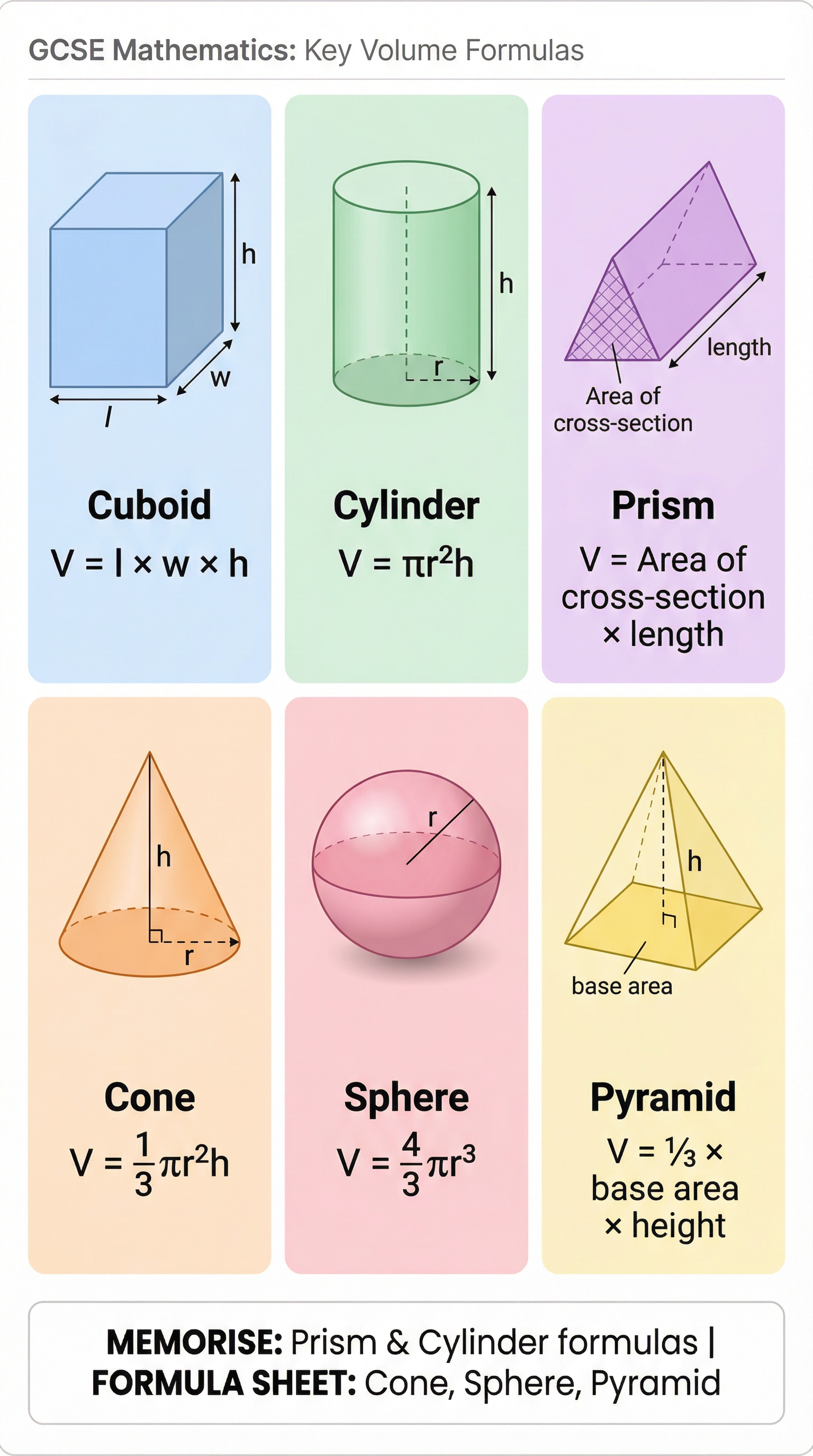
| Shape | Formula | Status on Formula Sheet |
|---|---|---|
| Prism | Area of cross-section × length | Must memorise |
| Cylinder | πr²h | Must memorise |
| Cone (Higher) | 1/3 πr²h | Given |
| Sphere (Higher) | 4/3 πr³ | Given |
| Pyramid (Higher) | 1/3 × base area × height | Given |
Unit Conversions:
- Length: 1 m = 100 cm
- Area: 1 m² = 100² cm² = 10,000 cm²
- Volume: 1 m³ = 100³ cm³ = 1,000,000 cm³
A very common mistake is to use a conversion factor of 100 for volume.
Practical Applications
Volume calculations are used everywhere in the real world, which is why they are tested so heavily. Think about:
- Engineering: Calculating the capacity of water tanks, fuel tanks, or concrete supports.
- Packaging: Designing boxes and containers that hold a specific amount of product while minimising material waste.
- Cooking: Measuring ingredients and understanding the capacity of pots and pans.
- Medicine: Calculating the volume of organs or the dosage of medication.