Study Notes
Overview
Trigonometry is a fundamental branch of mathematics that explores the relationships between the angles and side lengths of triangles. For your AQA GCSE exam, this topic is a significant source of marks, testing your ability to apply core principles to a variety of problems, from simple 2D shapes to complex 3D structures. A strong grasp of trigonometry is not just about memorising formulas; it's about developing the problem-solving skills to select the right tool for the job, a skill highly valued by examiners. This topic connects directly to geometry, Pythagoras' theorem, and vectors, often appearing in multi-step questions that require you to bring together knowledge from different areas of the specification. Expect to see questions ranging from straightforward calculations to 'show that' reasoning problems and real-world applications.
Key Concepts
Concept 1: Right-Angled Trigonometry (SOH CAH TOA)
The foundation of all trigonometry starts with the right-angled triangle. The three primary trigonometric ratios – Sine, Cosine, and Tangent – are defined by the ratios of the lengths of the sides relative to a specific angle (θ).
To identify the sides, always start by finding the Hypotenuse, which is the longest side and is always opposite the right angle. Then, relative to the angle θ:
- The Opposite side is directly across from the angle θ.
- The Adjacent side is next to the angle θ (and is not the Hypotenuse).
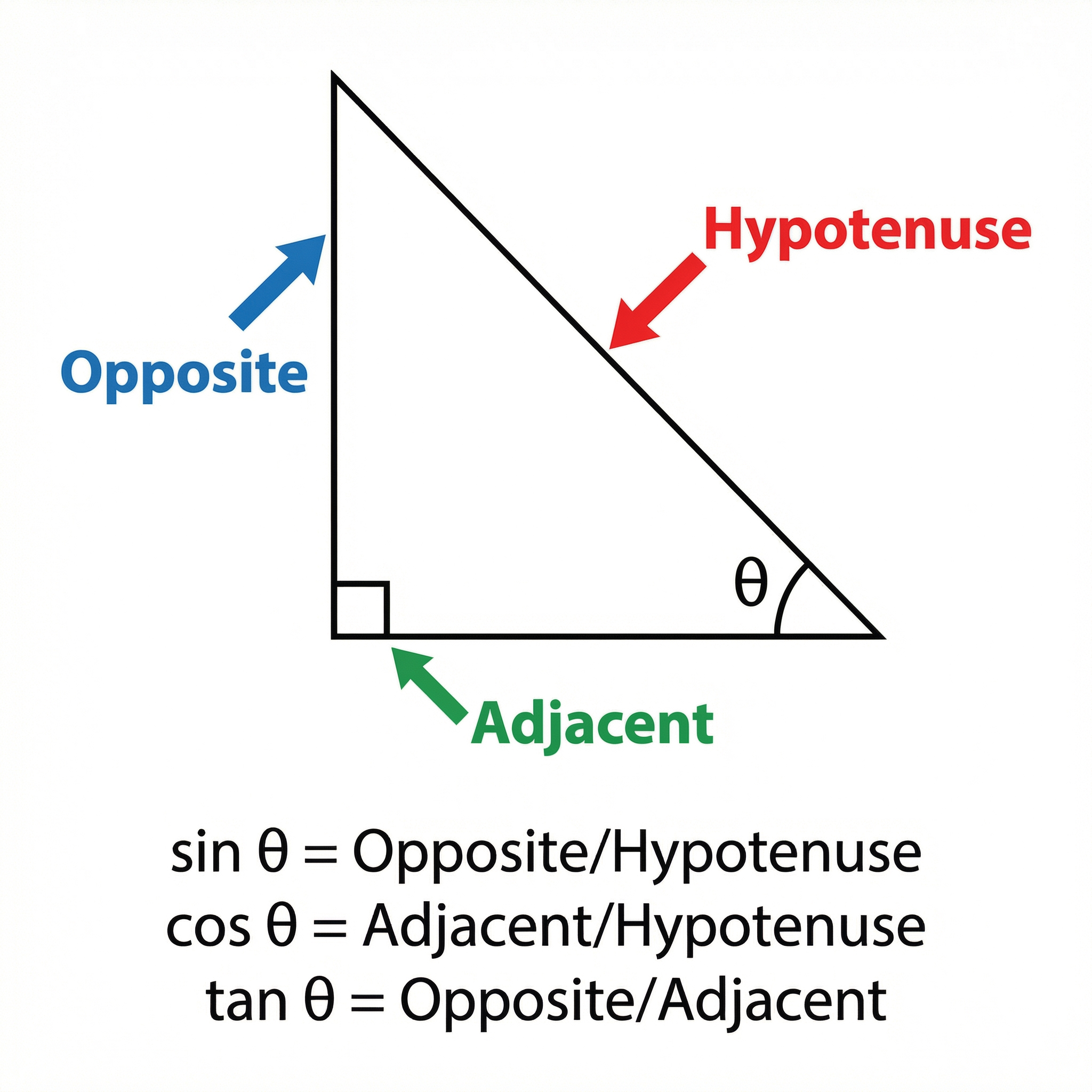
The mnemonic SOH CAH TOA is essential for recalling these ratios:
- SOH: Sine(θ) = Opposite / Hypotenuse
- CAH: Cosine(θ) = Adjacent / Hypotenuse
- TOA: Tangent(θ) = Opposite / Adjacent
These ratios allow you to find an unknown side length if you know one side and an angle, or find an unknown angle if you know two side lengths. To find an angle, you use the inverse trigonometric functions on your calculator: sin⁻¹, cos⁻¹, and tan⁻¹.
Concept 2: The Sine and Cosine Rules (Higher Tier Only)
When a triangle does not have a right angle, SOH CAH TOA cannot be used. For these non-right-angled triangles, Higher Tier candidates must use the Sine Rule and the Cosine Rule.
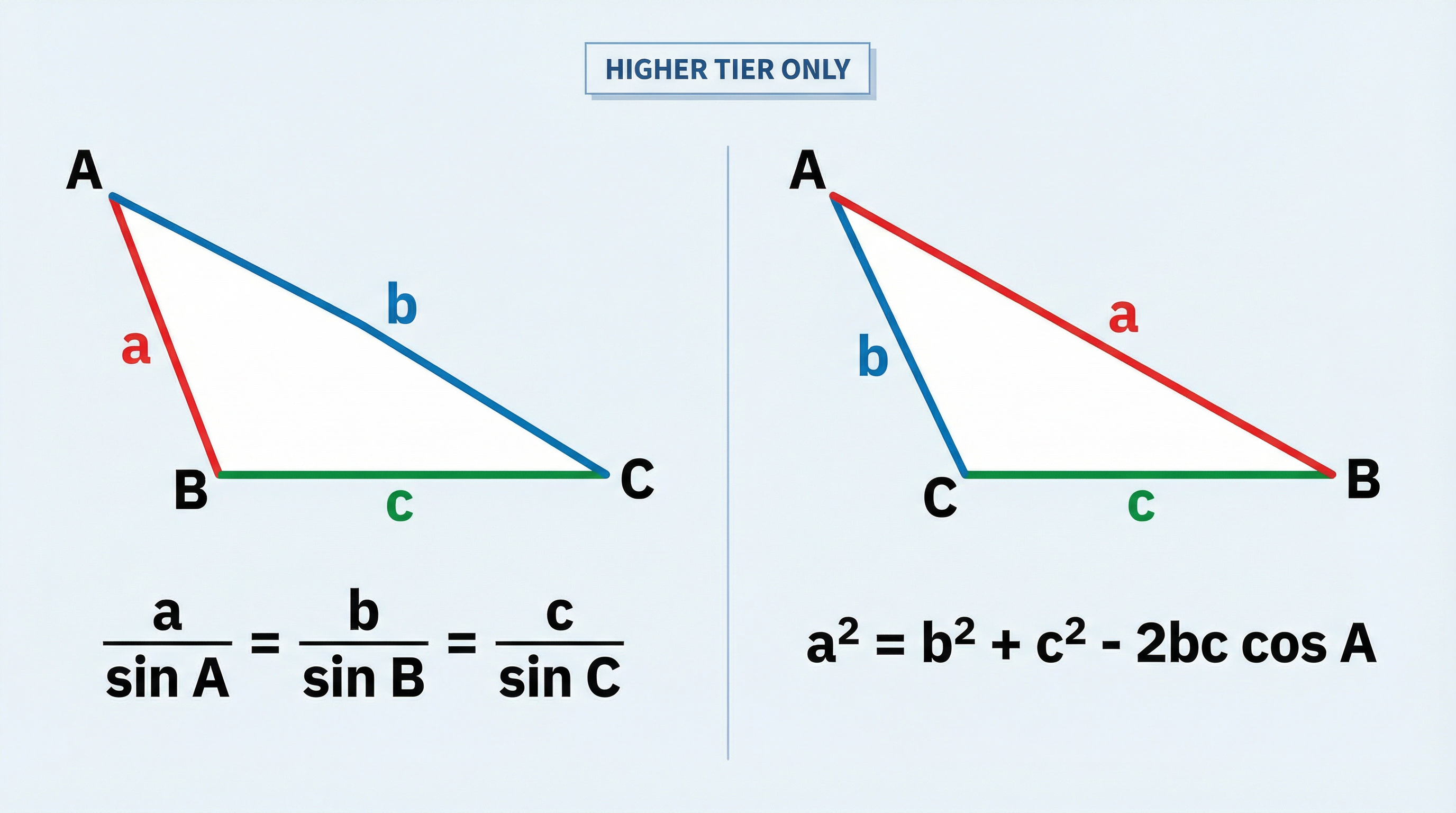
The Sine Rule is used when you know:
- Two angles and any side (AAS or ASA)
- Two sides and a non-included angle (SSA) - be aware this can sometimes lead to an ambiguous case, though this is rare at GCSE.
The rule states that the ratio of the length of a side to the sine of its opposite angle is constant for all three sides:
a/sin A = b/sin B = c/sin C
The Cosine Rule is used when you know:
- Two sides and the included angle (SAS) to find the third side.
- All three sides (SSS) to find any angle.
There are two forms of the rule:
- To find a side: a² = b² + c² - 2bc cos A
- To find an angle (rearranged): cos A = (b² + c² - a²) / 2bc
Concept 3: Area of a Triangle using Sine (Higher Tier Only)
Another tool for non-right-angled triangles is the formula for the area, which uses the sine of an included angle. This is often more direct than finding a perpendicular height.
Area = ½ ab sin CHere, C is the angle included between sides a and b. You need to know two sides and the angle between them. This formula is provided on the AQA formula sheet.
Concept 4: 3D Trigonometry (Higher Tier Only)
3D trigonometry problems require you to visualise and extract 2D right-angled triangles from a 3D shape (like a cuboid, pyramid, or prism). The key skill is identifying the correct triangle to solve the problem. Common tasks include finding the length of a space diagonal or the angle between a line and a plane.
To find the angle between a line and a plane, you must find the angle between the line and its projection onto the plane. This involves dropping a perpendicular from a point on the line to the plane, forming a right-angled triangle. An essential exam technique is to redraw the relevant 2D triangle separately, labelling the vertices and known lengths/angles. This simplifies the problem and reduces the chance of errors.
Mathematical Relationships
| Formula | Tier | When to Use | Given on Formula Sheet? |
|---|---|---|---|
| SOH CAH TOA | Both | Right-angled triangles only. | No (Must memorise) |
| Pythagoras' Theorem: a² + b² = c² | Both | Right-angled triangles (to find a side from two other sides). | Yes |
| Sine Rule: a/sin A = b/sin B | Higher | Non-right-angled triangles (AAS, SSA). | Yes |
| Cosine Rule: a² = b² + c² - 2bc cos A | Higher | Non-right-angled triangles (SAS, SSS). | Yes |
| Area = ½ ab sin C | Higher | Area of any triangle when you know two sides and the included angle. | Yes |
Practical Applications
Trigonometry is not just an abstract topic; it is the mathematical foundation for many real-world fields. Surveyors use it to measure distances and elevations of land, creating accurate maps. Astronomers use it to calculate the distance to stars and planets. Engineers rely on it to design structures like bridges and buildings, ensuring they can withstand forces. It is also fundamental to navigation (GPS), computer graphics (creating 3D models in games and movies), and physics (analysing waves and forces). Understanding these applications can provide context and make the formulas more memorable.
