Study Notes

Overview
Data Handling is a cornerstone of mathematics, focusing on the collection, presentation, and analysis of information. For your OCR GCSE exam, this topic is crucial as it appears in every paper, testing your ability to not only construct statistical diagrams but also to critically interpret and compare them. This guide will take you from foundational concepts like bar charts and averages, essential for all candidates, to the more demanding Higher Tier topics such as histograms with unequal class widths and cumulative frequency analysis. By mastering these skills, you will be equipped to tackle a wide range of exam questions, from straightforward data representation to complex, multi-step problems requiring you to draw conclusions and justify your reasoning. A strong grasp of data handling is not just about passing your maths GCSE; it is about developing the critical thinking skills needed to understand and question the statistics you encounter every day.
Key Concepts
Concept 1: Averages and Measures of Spread
Understanding how to describe a dataset is fundamental. This involves calculating measures of central tendency (averages) and measures of spread (consistency).
- Mean: The sum of all data points divided by the number of data points. It gives a good overall picture but can be skewed by extreme values (outliers).
- Median: The middle value when the data is arranged in order. It is not affected by outliers, making it a robust measure of the average.
- Mode: The most frequently occurring value. A dataset can have one mode (unimodal), two modes (bimodal), or more.
- Range: The difference between the highest and lowest values. It is a simple measure of spread but can be misleading if there are outliers.
- Interquartile Range (IQR): The difference between the upper quartile (Q3) and the lower quartile (Q1). It measures the spread of the middle 50% of the data and is not affected by outliers, making it a more reliable measure of spread than the range.
Concept 2: Grouped Frequency Tables
Often, data is presented in groups or classes (e.g., 10 < h ≤ 20). You need to be able to work with this format.
- Modal Class: The class with the highest frequency.
- Estimate of the Mean: You cannot find the exact mean from grouped data. Instead, you calculate an estimate by assuming every value in a class is equal to the midpoint. The formula is: Estimated Mean = Σ(f × x) / Σf, where 'f' is the frequency and 'x' is the midpoint of the class.
Concept 3: Histograms (Higher Tier)
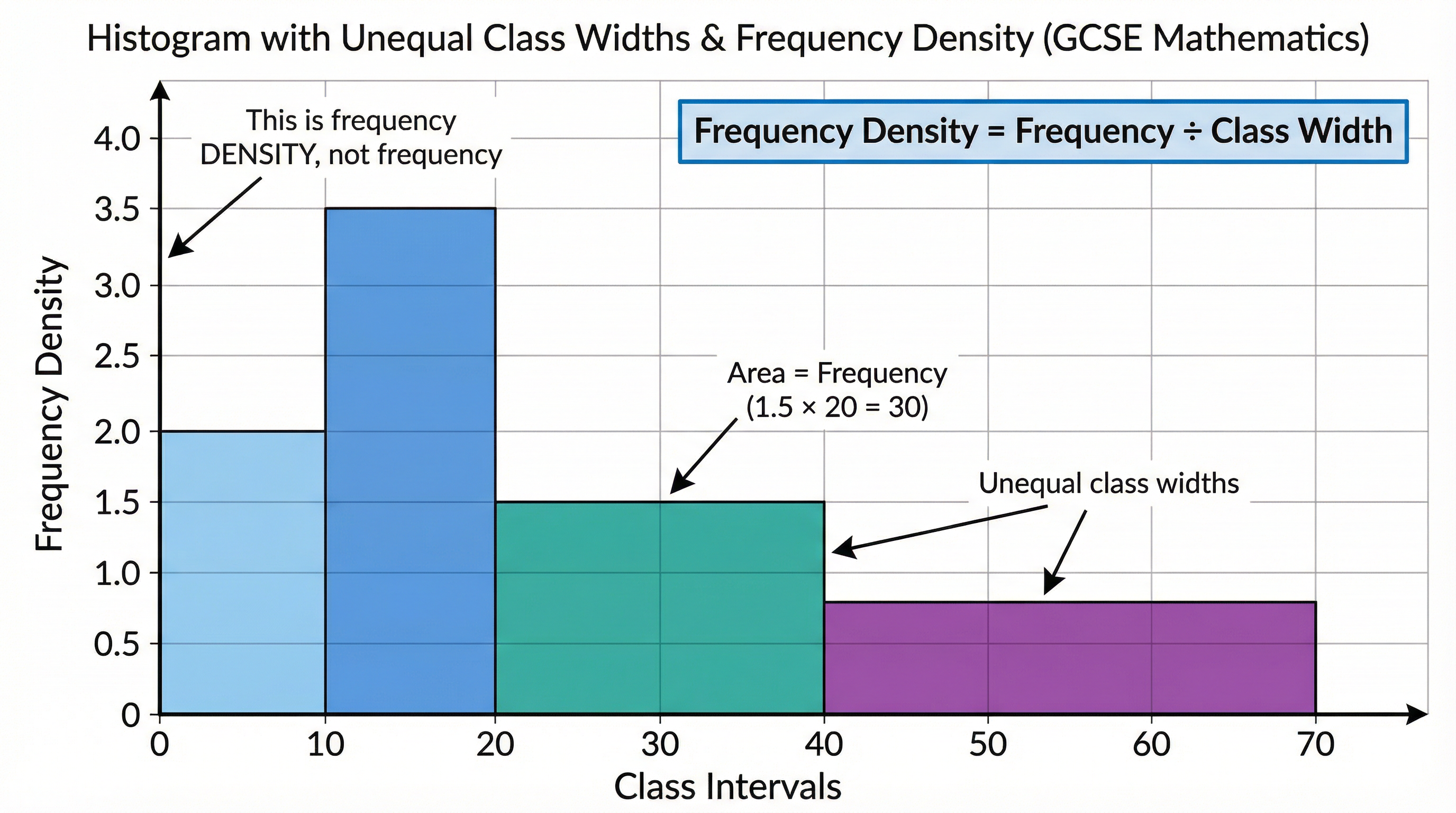
Histograms are used to represent continuous data. For GCSE Higher Tier, you must be able to handle histograms with unequal class widths. This is a common area where marks are lost.
- Key Principle: In a histogram, the area of the bar represents the frequency.
- Frequency Density: Because Area = Frequency, it follows that Height = Frequency / Width. This 'height' is called Frequency Density. You MUST plot Frequency Density on the y-axis.
- Formula: Frequency Density = Frequency / Class Width
Concept 4: Cumulative Frequency (Higher Tier)
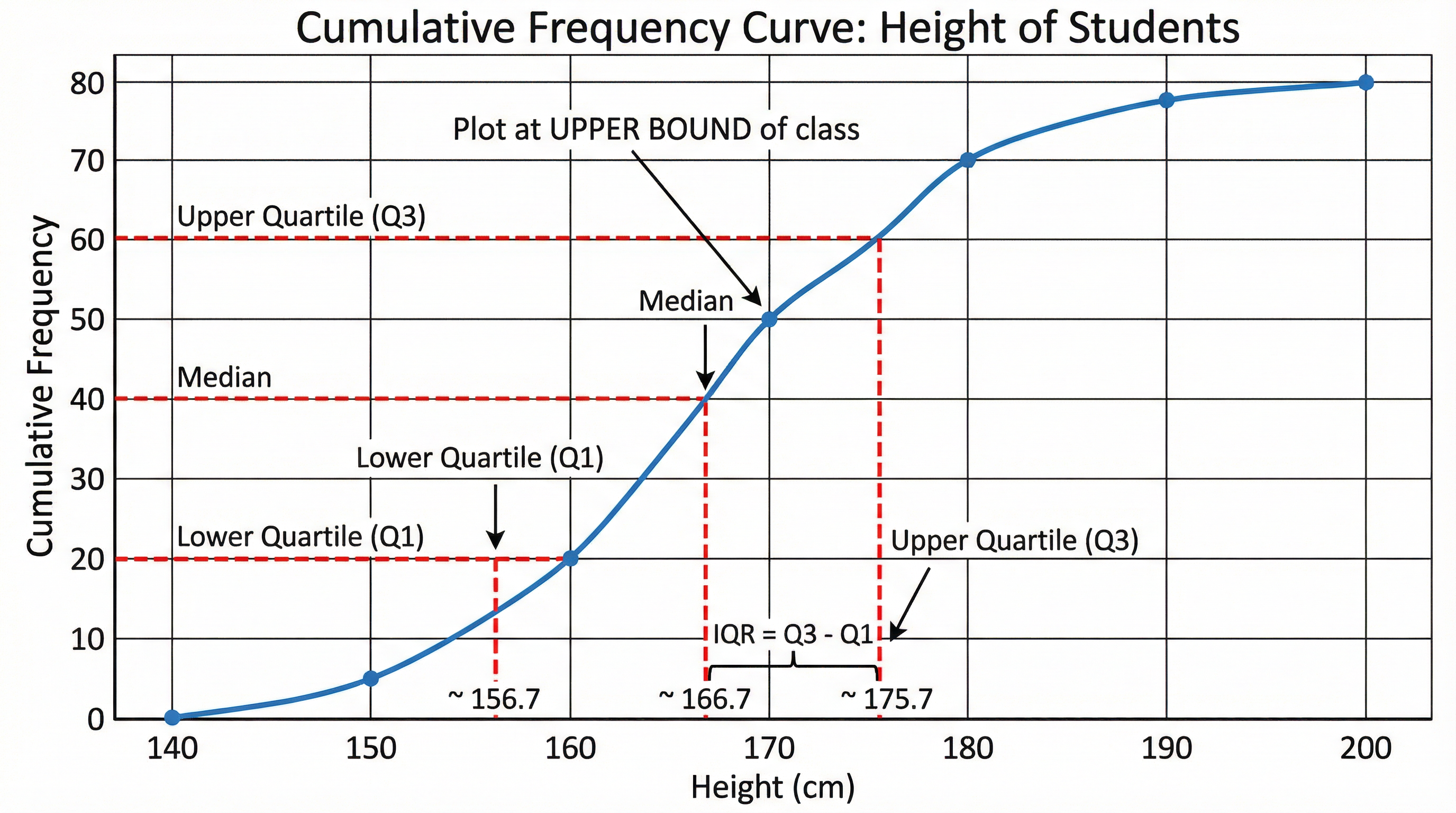
Cumulative frequency is the running total of the frequencies. A cumulative frequency graph is a powerful tool for estimating the median and quartiles.
- Plotting: Always plot the cumulative frequency at the upper bound of each class interval.
- Shape: The graph should be a smooth 'S'-shaped curve.
- Estimating Values: You can use the graph to find the median (at 50% of the total frequency), the lower quartile (at 25%), and the upper quartile (at 75%).
Concept 5: Box Plots (Higher Tier)
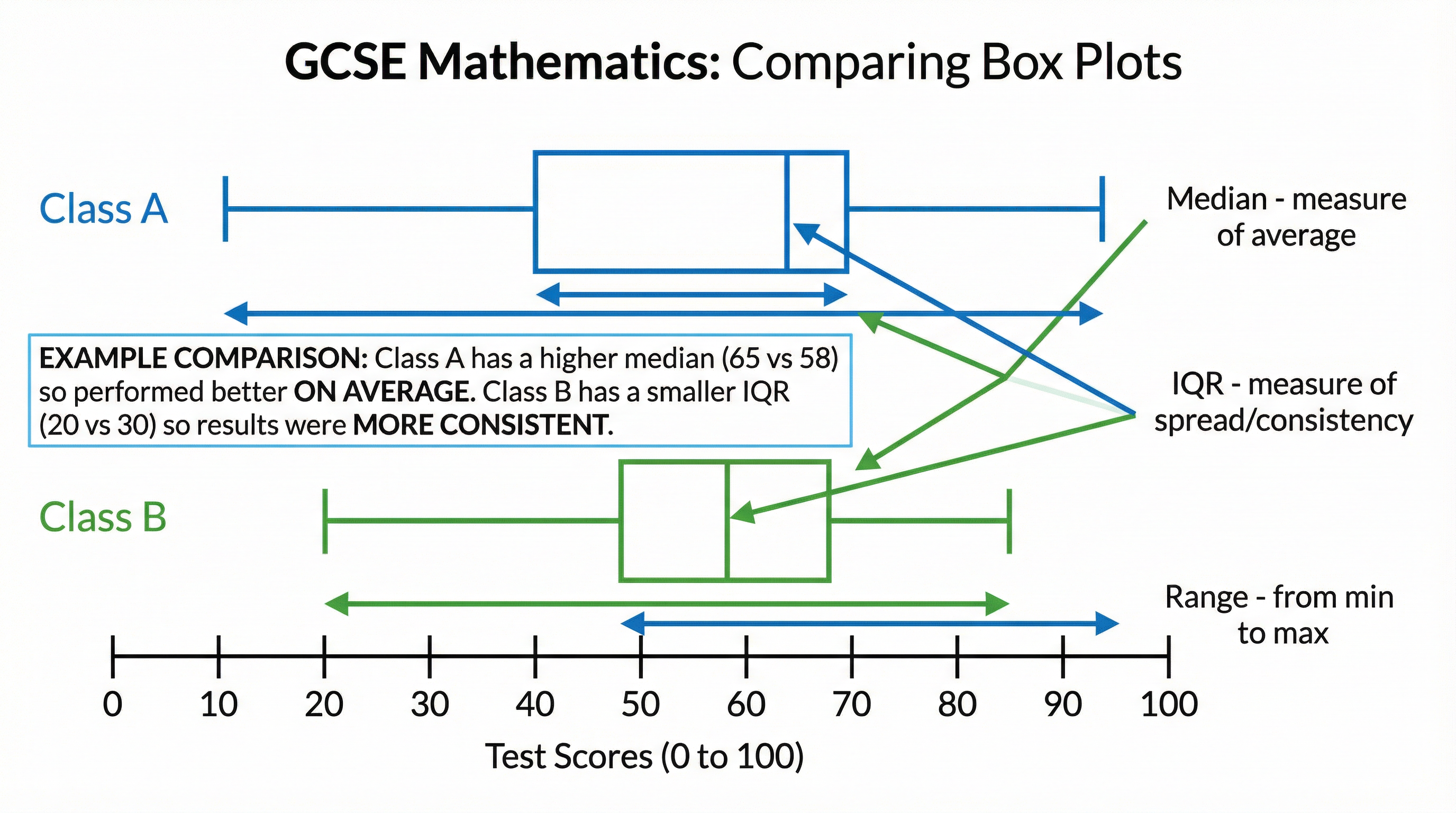
Box plots (or box-and-whisker diagrams) are a visual representation of the five-figure summary: Minimum, Lower Quartile (Q1), Median (Q2), Upper Quartile (Q3), and Maximum.
- Comparison: They are excellent for comparing two or more datasets. When comparing, you MUST comment on both a measure of location (the median) and a measure of spread (the IQR or range).
Mathematical/Scientific Relationships
- Estimated Mean from Grouped Data:
x̄ ≈ Σ(f × x) / Σf(Must memorise) - Frequency Density:
Frequency Density = Frequency / Class Width(Must memorise) - Interquartile Range (IQR):
IQR = Q3 - Q1(Must memorise)
Practical Applications
Data handling is used everywhere, from analysing business performance and scientific experiments to understanding social trends. For example, the Office for National Statistics (ONS) uses these techniques to analyse census data, helping the government to plan for services like schools and hospitals. In business, a company might use box plots to compare the performance of two different sales teams. Understanding how to critically read a chart is a vital life skill to avoid being misled by biased or poorly constructed graphics in the media.
