Study Notes

Overview
Fractions, Decimals, and Percentages (FDP) are the three different ways of representing parts of a whole. Mastery of this topic is not just about performing calculations; it's about developing fluency and understanding the relationships between these forms. In your OCR GCSE Mathematics exam, you will be expected to move seamlessly between them, applying your knowledge to a wide range of problems, from simple arithmetic to complex financial calculations. This topic forms the bedrock of many other areas in mathematics, such as ratio, proportion, and probability. Examiners will test your ability to perform calculations without a calculator, as well as your problem-solving skills in contextual scenarios on calculator papers. Expect to see questions on finding fractions or percentages of amounts, percentage increases and decreases, and the more challenging reverse percentages.
Key Concepts
Concept 1: The FDP Connection
Fractions, decimals, and percentages are fundamentally linked. A fraction represents a part of a whole (e.g., 1/2), a decimal represents the same part in base-10 (e.g., 0.5), and a percentage represents that part per hundred (e.g., 50%). Understanding how to convert between them is a critical skill. To convert a fraction to a decimal, you divide the numerator by the denominator. To convert a decimal to a percentage, you multiply by 100. To convert a percentage back to a fraction, you write it over 100 and simplify.
Example: Convert 3/4 to a decimal and a percentage.
- Decimal: 3 ÷ 4 = 0.75
- Percentage: 0.75 × 100 = 75%

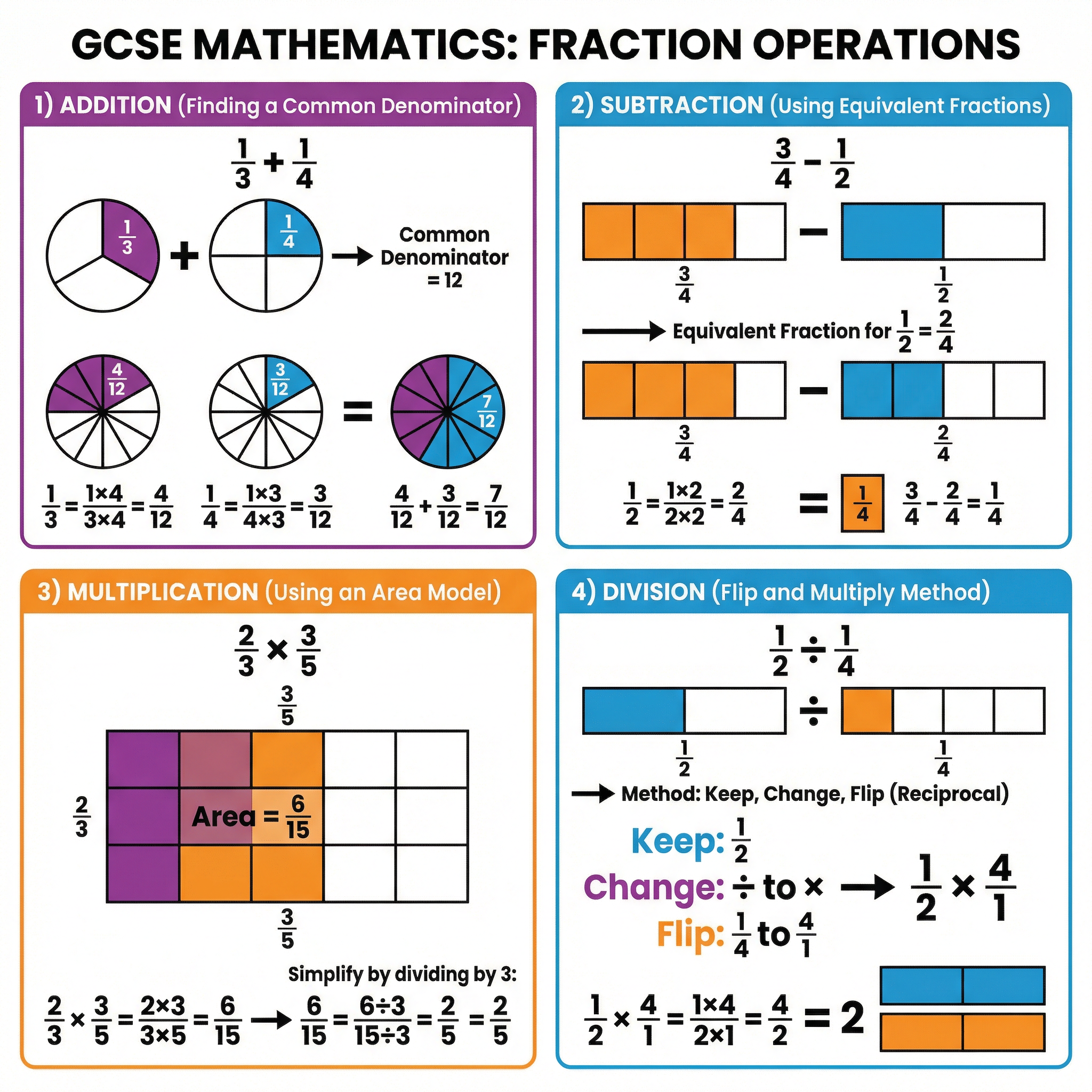
Concept 2: Fraction Arithmetic
Candidates must be proficient in the four basic operations with fractions: addition, subtraction, multiplication, and division. For addition and subtraction, the key is to find a common denominator. For multiplication, you simply multiply the numerators and the denominators. For division, you use the 'Keep, Change, Flip' method, where you keep the first fraction, change the division to multiplication, and flip the second fraction (find its reciprocal).
Example: Calculate 2/5 + 1/3.
- Find a common denominator: 15
- Convert the fractions: (2×3)/(5×3) + (1×5)/(3×5) = 6/15 + 5/15
- Add the numerators: 11/15
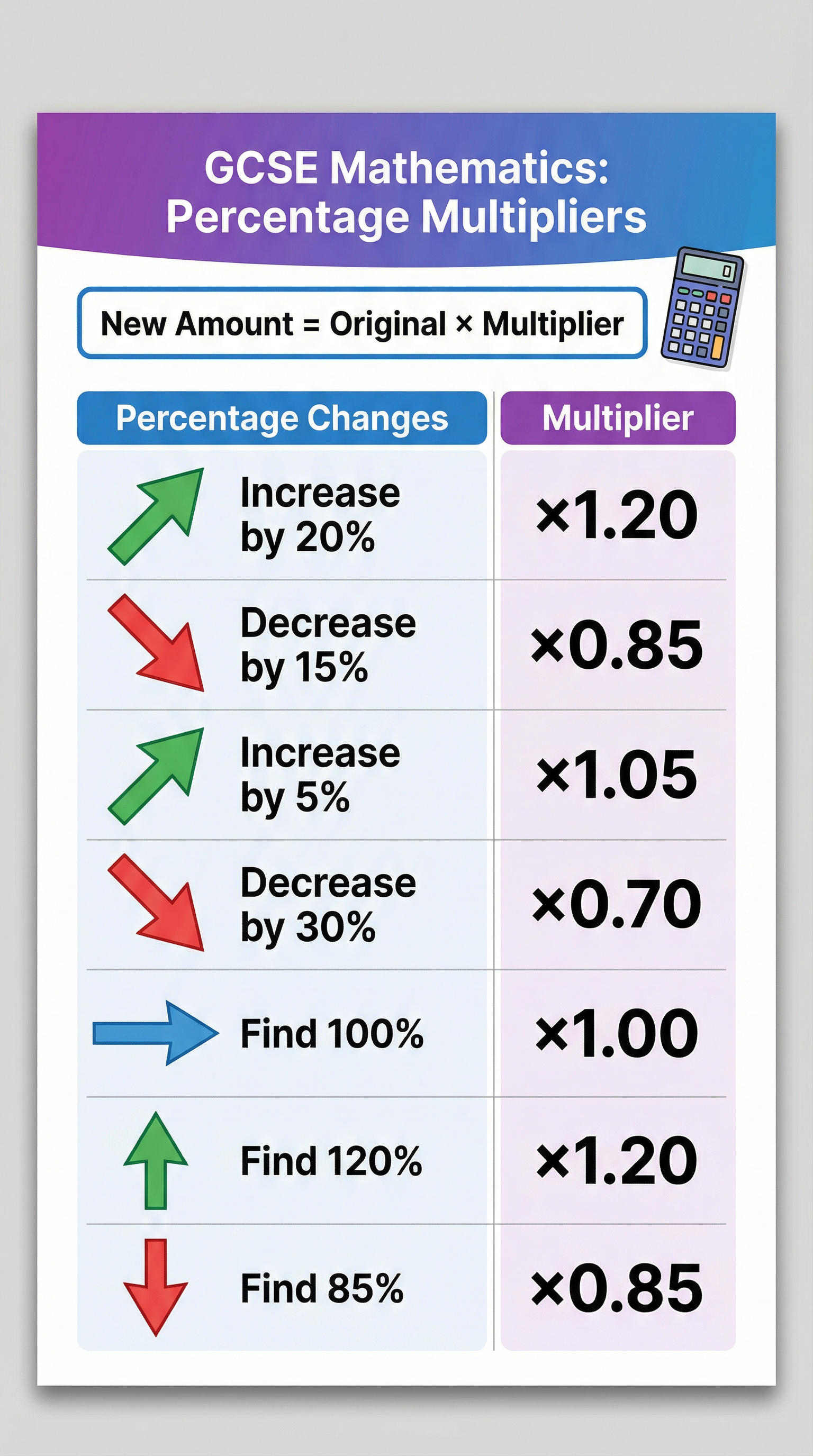
Concept 3: Percentage Multipliers
For percentage calculations, especially on calculator papers, using decimal multipliers is the most efficient and least error-prone method. An increase of P% corresponds to a multiplier of (1 + P/100), while a decrease of P% corresponds to a multiplier of (1 - P/100). This method is particularly powerful for compound interest and reverse percentage problems.
Example: Increase £60 by 15%.
- The multiplier is 1 + 15/100 = 1.15
- New amount = £60 × 1.15 = £69
Concept 4: Reverse Percentages
A common source of error is the reverse percentage problem, where you are given the final amount after a percentage change and asked to find the original amount. The key is to set up an algebraic equation using the multiplier. If a price was increased by 20% to £240, the original price (x) is found by solving 1.20x = £240, which means x = £240 ÷ 1.20 = £200. The mistake to avoid is calculating 20% of £240 and subtracting it.
Example: A coat is in a sale with 30% off. The sale price is £84. What was the original price?
- A 30% decrease means you have 70% of the original price.
- The multiplier is 0.70.
- 0.70 × Original Price = £84
- Original Price = £84 ÷ 0.70 = £120
Mathematical/Scientific Relationships
- Fraction to Decimal: Numerator ÷ Denominator
- Decimal to Percentage: Decimal × 100
- Percentage to Fraction: Percentage / 100 (and simplify)
- Percentage Increase: New Amount = Original Amount × (1 + Percentage/100)
- Percentage Decrease: New Amount = Original Amount × (1 - Percentage/100)
- Percentage Change: (Difference / Original) × 100
- Compound Interest: A = P(1 + r/n)^(nt), where A is the future value, P is the principal, r is the annual interest rate, n is the number of times interest is compounded per year, and t is the number of years. For GCSE, you are more likely to perform year-on-year calculations.
Practical Applications
FDP is everywhere in the real world, which is why it's tested so heavily in context. You'll see it in:
- Shopping: Discounts, sales tax (VAT), and special offers.
- Finance: Interest rates on savings accounts and loans, inflation, and profit margins.
- Statistics: Representing data in charts and graphs.
- Science: Calculating concentrations of solutions or percentage yields in experiments.
- Everyday Life: Splitting a bill, understanding nutritional information on food packaging, or following a recipe.
