Algebraic expressions (simplifying, expanding, factorising)

Overview

Algebraic expressions form the backbone of GCSE Mathematics, appearing in nearly every paper and accounting for a substantial proportion of available marks. This topic focuses on three core manipulative skills: simplifying expressions by collecting like terms, expanding brackets to eliminate parentheses, and factorising to rewrite expressions in their most compact form. These skills are not isolated; they are the foundation for solving equations, working with formulae, graphing functions, and tackling multi-step problem-solving questions. At Foundation tier, candidates are expected to simplify linear expressions and expand single brackets, while Higher tier extends to expanding double brackets, factorising quadratics, and manipulating algebraic fractions. The WJEC specification emphasises procedural fluency and the ability to show clear, logical working, particularly in 'Show that' questions where reasoning marks are awarded. Understanding the underlying structure of algebraic expressions, recognising patterns, and applying systematic methods will enable candidates to approach these questions with confidence and precision.

Key Concepts

Concept 1: Simplifying Expressions by Collecting Like Terms

Simplifying an algebraic expression means combining terms that are alike to produce the most concise form. Like terms are terms that contain exactly the same variable or combination of variables raised to the same power. For example, 3x and 7x are like terms because they both contain the variable x raised to the power of 1. However, 3x and 3x² are not like terms because the powers of x differ. Similarly, 2xy and 5xy are like terms, but 2xy and 2x are not.

The process of simplifying involves identifying all like terms in an expression and adding or subtracting their coefficients. Consider the expression 5a + 3b - 2a + 7b. To simplify, first identify the like terms: 5a and -2a are like terms, as are 3b and 7b. Combining these gives (5 - 2)a + (3 + 7)b = 3a + 10b. A critical technique recommended by examiners is to circle or underline like terms, ensuring that the sign immediately preceding each term is included. This prevents common errors, particularly with subtraction.

Example: Simplify 4x² + 2x - 3x² + 5x - 1.

First, identify like terms: 4x² and -3x² are like terms, and 2x and 5x are like terms. The constant -1 stands alone. Combining: (4 - 3)x² + (2 + 5)x - 1 = x² + 7x - 1.

A frequent mistake is confusing addition with multiplication. Candidates often write a + a = a², which is incorrect. The correct simplification is a + a = 2a. Multiplication of like terms follows different rules: a × a = a² because you multiply the coefficients and add the exponents.

Concept 2: Expanding Brackets

Expanding brackets, also known as removing brackets or distributing, involves multiplying every term inside a bracket by the term outside. This is a fundamental skill that appears in both Foundation and Higher tier papers. For a single bracket, such as 3(2x + 5), you multiply the 3 by each term inside: 3 × 2x = 6x and 3 × 5 = 15, giving 6x + 15.

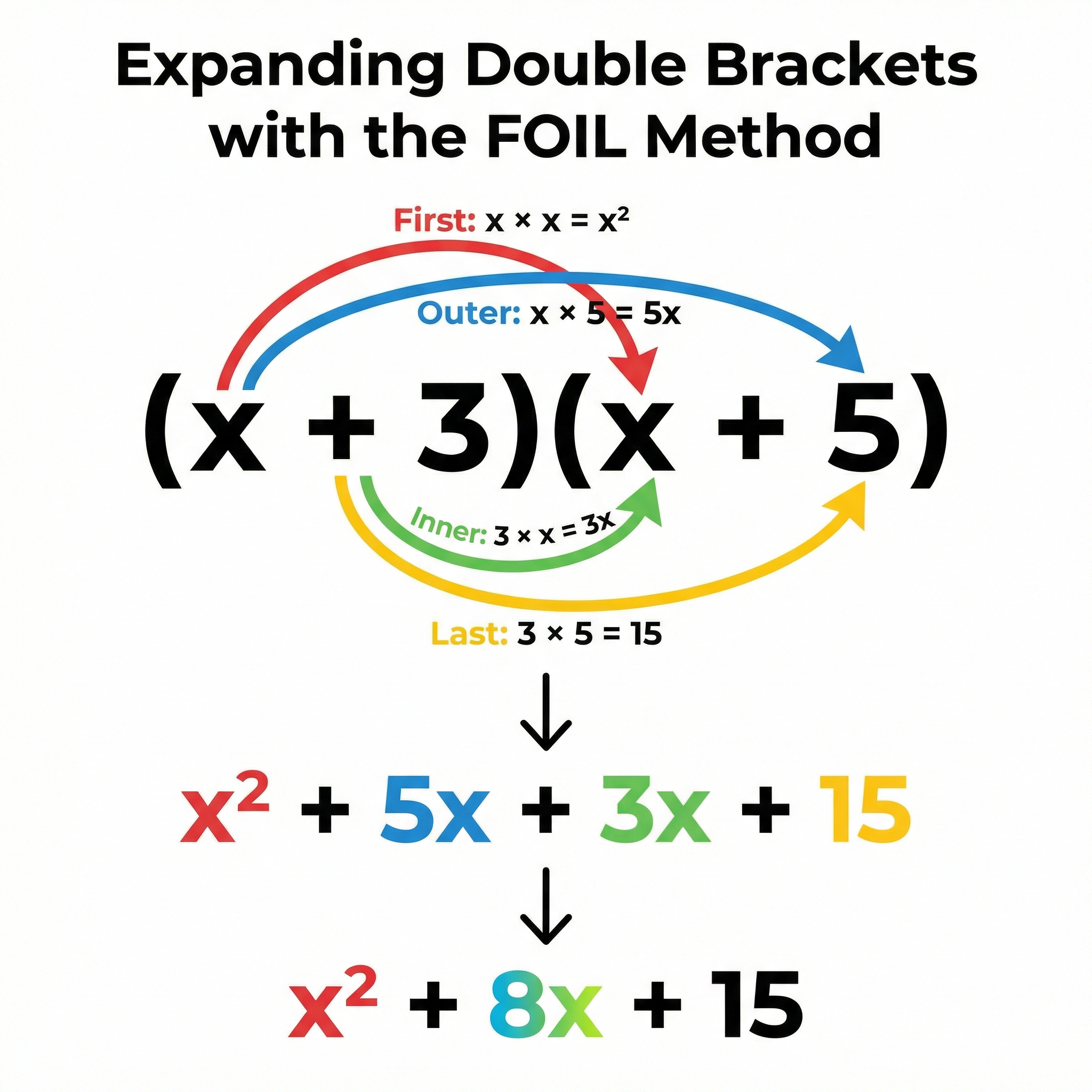
For double brackets, such as (x + 3)(x + 5), the process is more involved. A widely taught method is FOIL, which stands for First, Outer, Inner, Last. This mnemonic ensures that all four products are calculated:

• First: Multiply the first terms in each bracket: x × x = x²
• Outer: Multiply the outermost terms: x × 5 = 5x
• Inner: Multiply the innermost terms: 3 × x = 3x
• Last: Multiply the last terms in each bracket: 3 × 5 = 15

Writing these out gives x² + 5x + 3x + 15. The next step is to simplify by collecting like terms: 5x + 3x = 8x, so the final answer is x² + 8x + 15.

Example: Expand and simplify (x - 2)(x + 4).

Using FOIL:

• First: x × x = x²
• Outer: x × 4 = 4x
• Inner: -2 × x = -2x
• Last: -2 × 4 = -8

Combining: x² + 4x - 2x - 8 = x² + 2x - 8.

A critical error candidates make is squaring a bracket incorrectly. For example, (x + 3)² is often written as x² + 9, omitting the middle term. The correct expansion is (x + 3)(x + 3) = x² + 3x + 3x + 9 = x² + 6x + 9. This follows the pattern (a + b)² = a² + 2ab + b², known as the perfect square formula.

Concept 3: Factorising Expressions

Factorising is the reverse process of expanding. It involves rewriting an expression as a product of its factors, typically by placing common terms outside a bracket. The first step in any factorisation is to identify the highest common factor (HCF) of all terms. For example, in 6x + 9, the HCF is 3. Factorising gives 3(2x + 3) because 3 × 2x = 6x and 3 × 3 = 9.

For expressions involving variables, the HCF may include both a numerical coefficient and a variable. Consider 12x² + 18x. The HCF is 6x (the largest number dividing both 12 and 18, and the lowest power of x present in all terms). Factorising: 6x(2x + 3). Candidates often factorise incompletely, writing 2(6x² + 9x) or 6(2x² + 3x), which loses marks. Examiners award B1 for partial factorisation but require full factorisation for the A1 mark.

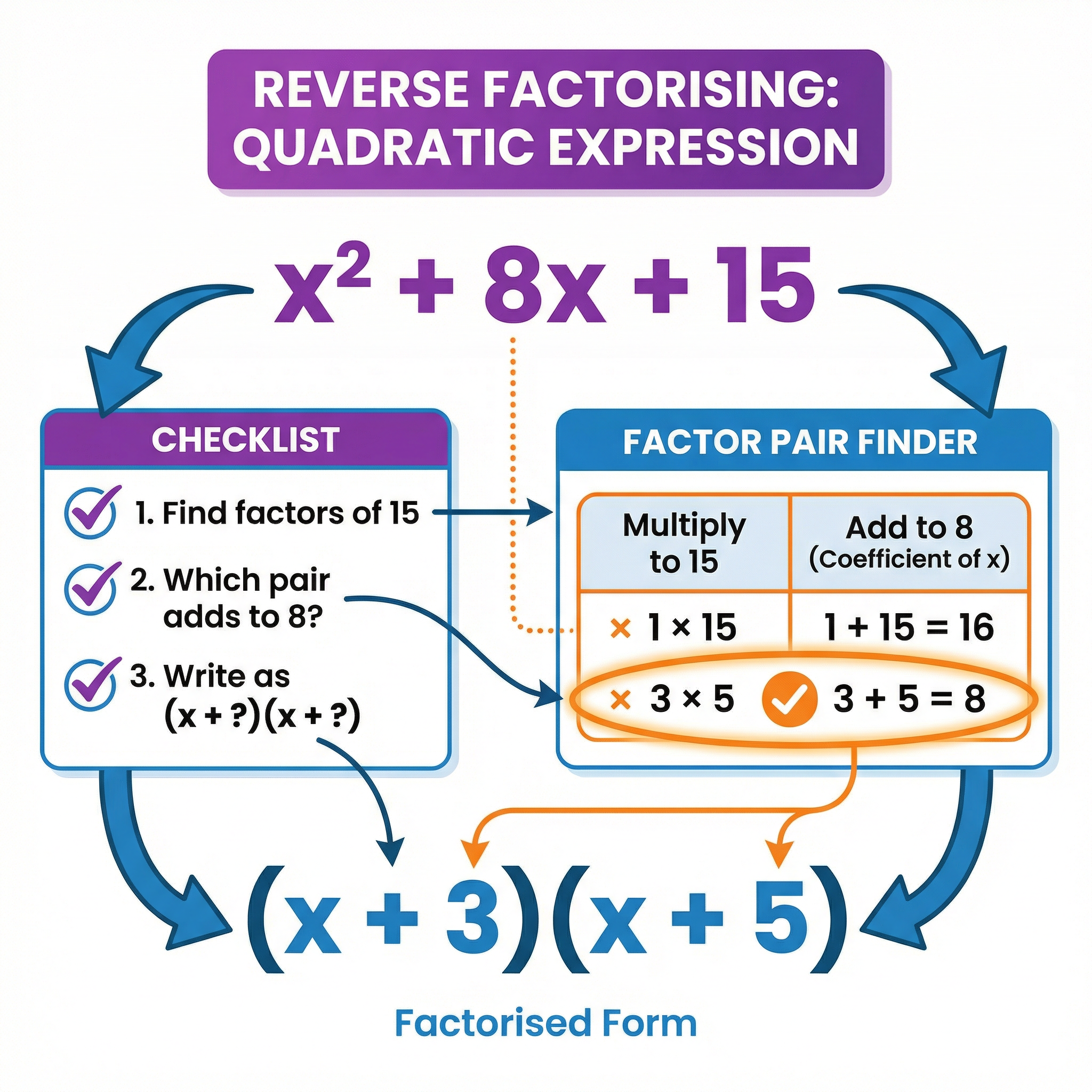
At Higher tier, candidates must factorise quadratic expressions of the form x² + bx + c. This requires finding two numbers that multiply to give c and add to give b. For example, to factorise x² + 8x + 15, list the factor pairs of 15: (1, 15) and (3, 5). Which pair adds to 8? The pair (3, 5). Therefore, x² + 8x + 15 = (x + 3)(x + 5). Always check your answer by expanding the brackets.

Example: Factorise fully x² - 5x + 6.

Find two numbers that multiply to +6 and add to -5. The pairs of 6 are (1, 6) and (2, 3). Since the sum must be negative and the product positive, both numbers must be negative: (-2, -3). Check: -2 × -3 = 6 and -2 + -3 = -5. Therefore, x² - 5x + 6 = (x - 2)(x - 3).

Concept 4: Algebraic Fractions

Algebraic fractions involve expressions in the numerator and denominator. Simplifying these requires factorising both parts completely before cancelling common factors. For example, to simplify (x² + 5x + 6) / (x + 2), first factorise the numerator: x² + 5x + 6 = (x + 2)(x + 3). The expression becomes [(x + 2)(x + 3)] / (x + 2). The common factor (x + 2) cancels, leaving x + 3.

Examiners stress that candidates must factorise fully before attempting to cancel. Cancelling terms rather than factors is a common error. For instance, in (x + 3) / (x + 5), the x terms cannot be cancelled because they are not factors; they are terms within a sum.

Mathematical/Scientific Relationships

Algebraic manipulation relies on the fundamental laws of arithmetic extended to variables:

• Commutative Law: a + b = b + a and ab = ba
• Associative Law: (a + b) + c = a + (b + c) and (ab)c = a(bc)
• Distributive Law: a(b + c) = ab + ac

The distributive law is the foundation of expanding brackets. When expanding (x + 3)(x + 5), you are applying the distributive law twice: first distributing (x + 3) over (x + 5), then distributing each term.

Index Laws (also called laws of exponents) are essential for simplifying expressions involving powers:

• xᵃ × xᵇ = xᵃ⁺ᵇ (multiply: add the exponents)
• xᵃ ÷ xᵇ = xᵃ⁻ᵇ (divide: subtract the exponents)
• (xᵃ)ᵇ = xᵃᵇ (power of a power: multiply the exponents)
• x⁰ = 1 (any number to the power of zero is 1)
• x⁻ᵃ = 1/xᵃ (negative exponent: reciprocal)

These laws must be memorised, as they are not provided on the formula sheet.

Perfect Square Formulas (must memorise):

• (a + b)² = a² + 2ab + b²
• (a - b)² = a² - 2ab + b²

Difference of Two Squares (must memorise, Higher tier):

• a² - b² = (a + b)(a - b)

This pattern is used to factorise expressions like x² - 9 = (x + 3)(x - 3).

Practical Applications

Algebraic expressions are used to model real-world situations where quantities vary. For example, if a plumber charges a call-out fee of £50 plus £30 per hour, the total cost C for h hours is given by the expression C = 50 + 30h. Simplifying, expanding, and factorising allow us to manipulate such expressions to solve problems, compare costs, and make predictions.

In geometry, the area of a rectangle with length (x + 5) and width (x + 3) is found by expanding: Area = (x + 5)(x + 3) = x² + 8x + 15. Conversely, if the area is given as x² + 8x + 15, factorising reveals the dimensions.

Algebraic manipulation is also foundational for calculus, physics, engineering, and computer science, where expressions are simplified and rearranged to solve equations and model systems.

Common Mistakes to Avoid

Candidates frequently lose marks due to recurring errors. Understanding these pitfalls and how to avoid them is as important as learning the correct methods.

Mistake 1: Confusing addition and multiplication. Writing a + a = a² instead of 2a. Remember: addition combines quantities, multiplication creates powers.

Mistake 2: Omitting the middle term when squaring. Writing (x + 3)² = x² + 9 instead of x² + 6x + 9. Always expand squared brackets using FOIL or the perfect square formula.

Mistake 3: Multiplying terms incorrectly. Writing 3x × 2x = 6x instead of 6x². When multiplying, multiply the coefficients and add the exponents.

Mistake 4: Incomplete factorisation. Writing 2(2x + 4) instead of 4(x + 2). Always extract the highest common factor.

Mistake 5: Sign errors when collecting like terms. Forgetting that the sign belongs to the term. Circle terms with their signs to avoid this.

Mistake 6: Cancelling terms instead of factors in fractions. In (x + 3)/(x + 5), the x terms cannot cancel because they are not factors.

Exam Technique

Time Per Mark

Approximately 1 to 1.5 minutes per mark. A 4-mark question on expanding and simplifying should take 4-6 minutes. If you are spending significantly longer, move on and return later.

Question Approach

1. Read the command word carefully. 'Simplify' means collect like terms. 'Expand' means remove brackets. 'Factorise' means put into brackets. 'Show that' means you must show intermediate steps.

2. Identify the skill being tested. Is it simplifying, expanding, or factorising? Sometimes a question combines multiple skills.

3. Write down your method. Even if you make an arithmetic error, method marks (M1) can be awarded if your approach is correct.

4. Check your answer. For factorisation, expand your answer to see if you get back to the original expression. For expansion, check that you have the correct number of terms.

Answer Structure

For 2-mark questions: Typically 1 mark for method, 1 mark for answer. Show at least one intermediate step.

For 3-4 mark questions: Show clear stages. For example, expanding double brackets: write the unsimplified expansion first (x² + 5x + 3x + 15), then the simplified form (x² + 8x + 15).

For 'Show that' questions: You must explicitly show the step before the final answer. If the question says 'Show that (x+3)(x+5) = x²+8x+15', you must write x² + 5x + 3x + 15 before writing the final line. This demonstrates reasoning and earns the R1 mark.

Common Pitfalls

• Not showing working: Even if your final answer is correct, you may lose method marks if no working is shown.
• Incorrect further simplification: If you have a correct answer but then simplify it incorrectly, you lose the accuracy mark.
• Leaving answers in non-standard form: Do not write 1x or x^1; write x. Do not write x + 0; write x.
• Forgetting to simplify after expanding: If you expand (x+2)(x+3) and write x² + 3x + 2x + 6 without simplifying to x² + 5x + 6, you may lose the final accuracy mark.

Command Word Strategies

• Simplify: Collect like terms. Combine terms with the same variable and power. Your answer should be as concise as possible.
• Expand: Multiply out the brackets. Use the distributive law. For double brackets, use FOIL.
• Factorise: Put into brackets. Find the highest common factor first. For quadratics, find two numbers that multiply to c and add to b.
• Show that: Demonstrate each step. Write the unsimplified form before the final answer. This is a reasoning question.
• Simplify fully or Factorise fully: Ensure you have extracted all common factors and combined all like terms. Partial answers do not earn full marks.