Study Notes
Overview
Data Representation (WJEC 4.2) is a cornerstone of the GCSE Mathematics curriculum, focusing on how we visually present and interpret numerical information. This topic is not just about drawing neat charts; it's about telling a story with data. Examiners are looking for candidates who can accurately construct a range of diagrams and, crucially, use them to make insightful comparisons and draw valid conclusions. From frequency polygons and cumulative frequency curves to the more demanding histograms with unequal class widths (Higher tier), mastering this area is essential for exam success. A strong grasp of data representation also provides a foundation for understanding probability and statistical testing, making it a key synoptic link across the specification. Expect to see questions that require you to both draw a chart from a table of data and interpret a given chart to find averages, spreads, or compare distributions.
Key Concepts
Concept 1: Frequency Polygons
A frequency polygon is used to represent grouped frequency data. Unlike a bar chart, it helps to show the shape of the distribution more clearly. The key principle is to plot frequency against the midpoint of each class interval. Once all points are plotted, they are joined with straight lines using a ruler to form a polygon. It is a common error to join the points with a smooth curve, which is incorrect and will lose marks. To complete the polygon, it should be anchored to the horizontal axis by extending the lines to the midpoints of the classes immediately before the first class and after the last class (where the frequency is zero).
Example: For a class interval of '10-20' with a frequency of 8, you would plot the point at (15, 8).
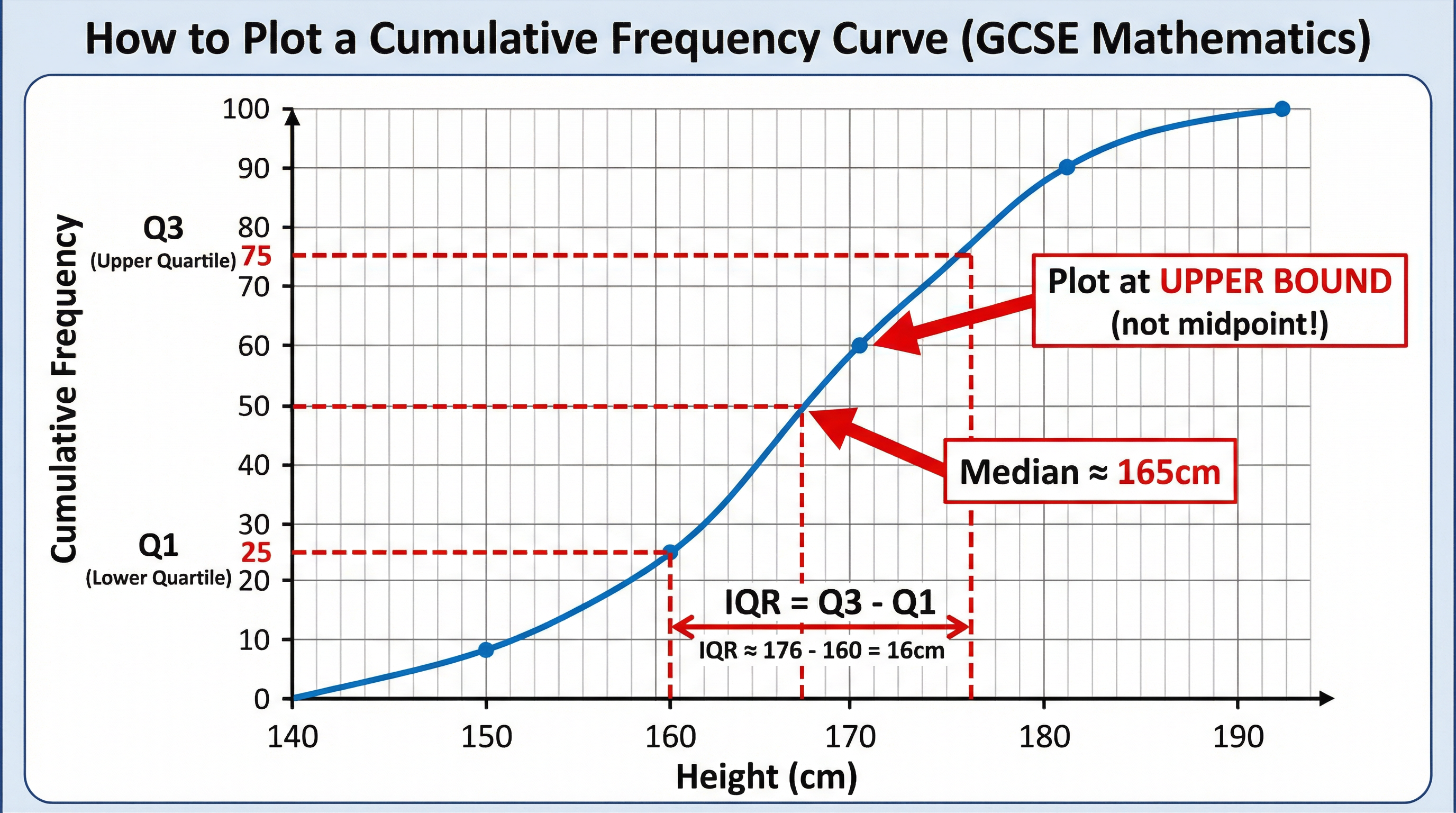
Concept 2: Cumulative Frequency Curves
Cumulative frequency is a running total of the frequencies. A cumulative frequency curve (or ogive) is a graphical representation of this information, which is particularly useful for estimating the median and quartiles of a distribution. The most critical rule for candidates to remember is that cumulative frequency values are plotted against the upper bound of each class interval, not the midpoint. A failure to do so is one of the most common mistakes. After plotting the points, they are joined with a smooth, S-shaped curve.
Example: If the cumulative frequency for the class '10-20' is 25, you plot the point at (20, 25).
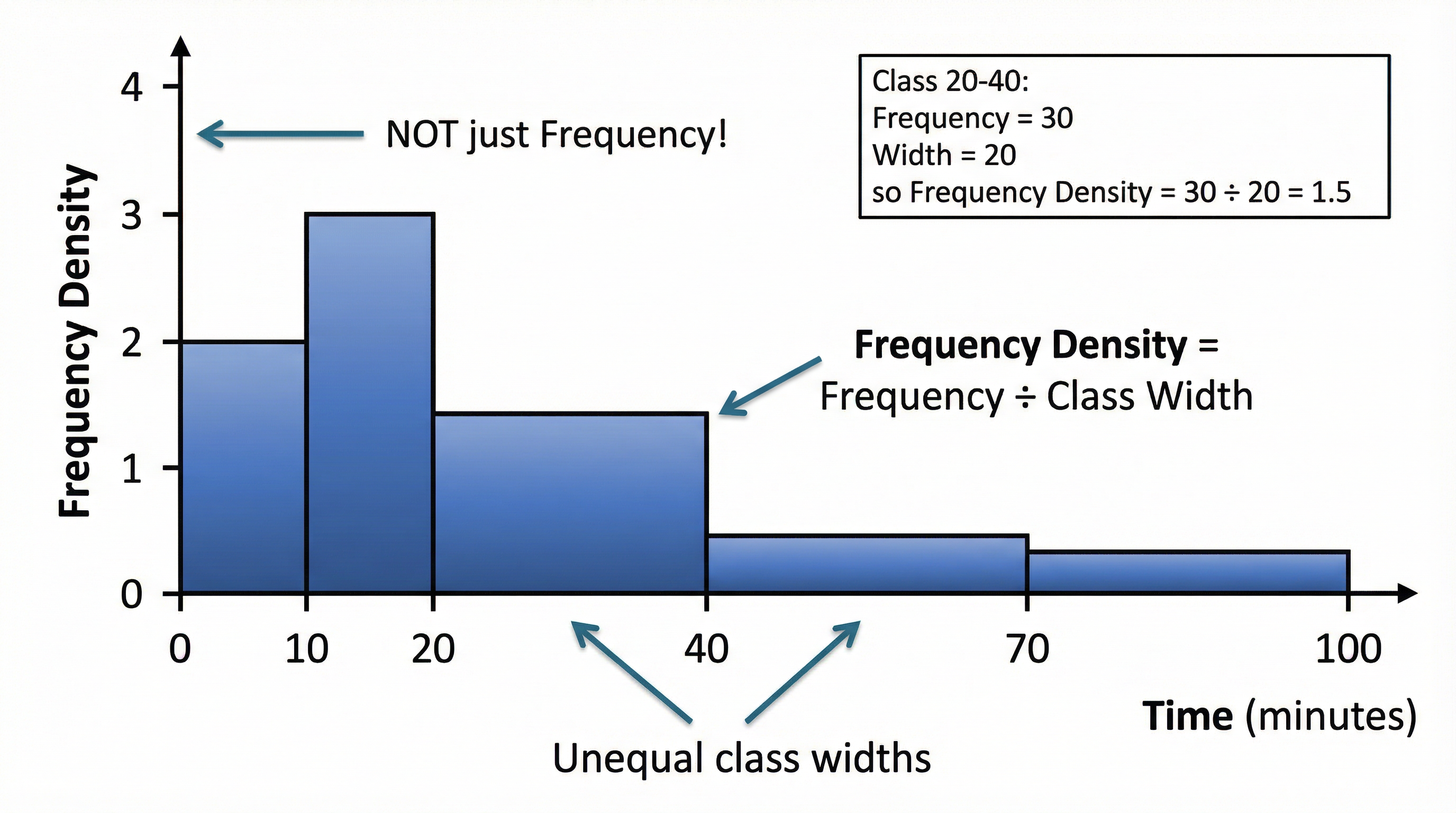
Concept 3: Histograms with Unequal Class Widths (Higher Tier Only)
Histograms are used for continuous data. While they look similar to bar charts, there are no gaps between the bars. For Higher tier candidates, a key challenge is constructing histograms where the class intervals have different widths. In this case, the height of each bar does not represent the frequency. Instead, we must calculate and plot the Frequency Density. The area of the bar (Frequency Density x Class Width) represents the frequency. The vertical axis must be labelled 'Frequency Density'.
Mathematical/Scientific Relationships
- Frequency Density:
Frequency Density = Frequency / Class Width(Must memorise) - Median from a Cumulative Frequency Curve: Find the value on the horizontal axis corresponding to 50% of the total frequency.
- Lower Quartile (Q1): Find the value corresponding to 25% of the total frequency.
- Upper Quartile (Q3): Find the value corresponding to 75% of the total frequency.
- Interquartile Range (IQR):
IQR = Q3 - Q1(Must memorise). This is a measure of spread or consistency.
Practical Applications
Data representation is used everywhere in the real world. Governments use it to present census data on population demographics. Scientists use it to show the results of experiments, for example, plotting the growth of plants over time. In business, sales figures are often represented using charts to track performance and identify trends. Understanding how to read and create these diagrams is a vital life skill for interpreting information presented in the media and making informed decisions.
