Scale drawings

Overview

Scale drawings are a fundamental part of applied mathematics, allowing us to represent large real-world objects and spaces in a manageable format. This topic, a cornerstone of the WJEC GCSE specification, tests your ability to work with ratio and proportion, measure accurately, and apply these skills to practical problems involving maps, floor plans, and bearings. It is a highly visual topic where precision is paramount; examiners expect candidates to be meticulous in their measurements and constructions. A strong grasp of scale drawings is not just about earning marks in this specific area; it provides a foundation for understanding concepts in geography, design technology, and even science. Typical exam questions range from straightforward calculations of real distances to more complex problems requiring you to construct diagrams or find locations based on multiple pieces of information. Often integrated into OCW (Organising, Communicating and Writing) questions, this topic is a prime opportunity to demonstrate clear, logical working and secure valuable communication marks.

Key Concepts

Concept 1: Understanding Scale

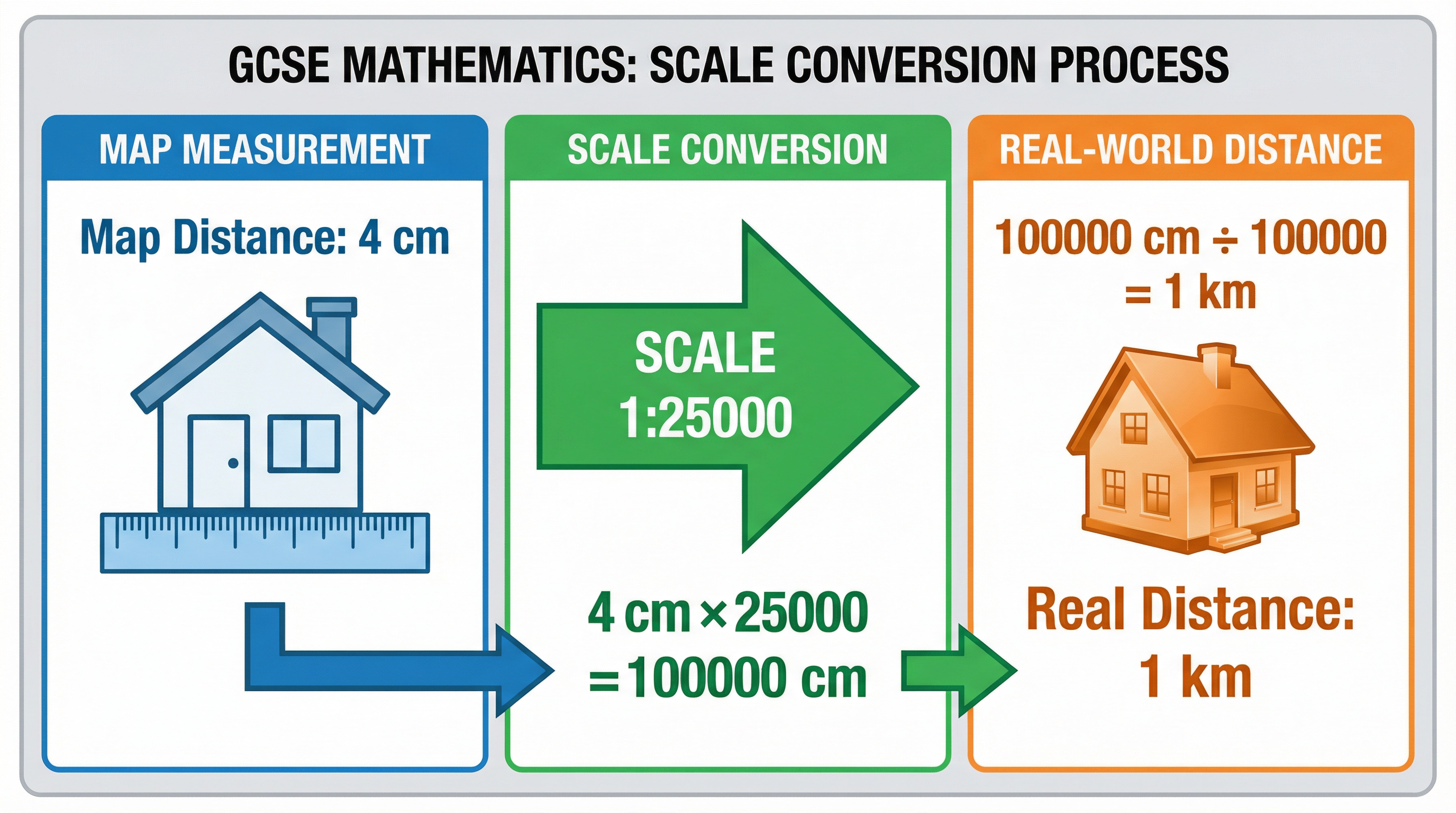
A scale is a ratio that compares the size of a drawing to the size of the real object. It's the crucial link between the representation and reality. You'll encounter scales in two main forms:

• Ratio Scale: This is written as 1:n, for example, 1:50 or 1:25000. This means that 1 unit of measurement on the drawing (like a centimetre) represents 'n' of the same units in the real world. For a scale of 1:50, 1 cm on the plan equals 50 cm in reality. This form is universal but requires careful unit conversion.

• Statement Scale: This is given as a direct relationship, such as 1 cm represents 2 km. This is often easier to use for initial calculations as the conversion is stated, but you must be vigilant with subsequent unit conversions (e.g., from km to m).

Example: A floor plan has a scale of 1:100. A room on the plan measures 5 cm long. To find the real length, you multiply the measured length by the scale factor: 5 cm * 100 = 500 cm. To make this more practical, you convert it to metres: 500 cm / 100 = 5 metres. The real room is 5 metres long.

Concept 2: Converting Between Map and Reality

This is the core skill in scale drawing questions. The direction of conversion determines whether you multiply or divide.

• Map to Reality: When you have a measurement from the drawing and want to find the actual size, you multiply by the scale factor.

• Reality to Map: When you know the actual size of an object and want to find how big it should be on your drawing, you divide by the scale factor.

Example: An architect wants to draw a 12-metre-long wall on a plan with a scale of 1:200. First, ensure units are consistent. 12 metres is 1200 cm. Now, apply the 'Reality to Map' rule: 1200 cm / 200 = 6 cm. The wall should be drawn 6 cm long on the plan.

Concept 3: Construction and Loci

Examiners often ask you to construct diagrams or find a point that satisfies certain conditions. This combines scale drawing with your knowledge of bearings and loci.

• Bearings: A bearing is an angle measured clockwise from the North direction, always given as a three-figure number (e.g., 045°, 120°). You will use a protractor to measure or draw these angles accurately.

• Construction: This involves using a ruler, protractor, and compass to create accurate diagrams. For example, finding a point that is a certain distance from one point and on a specific bearing from another.

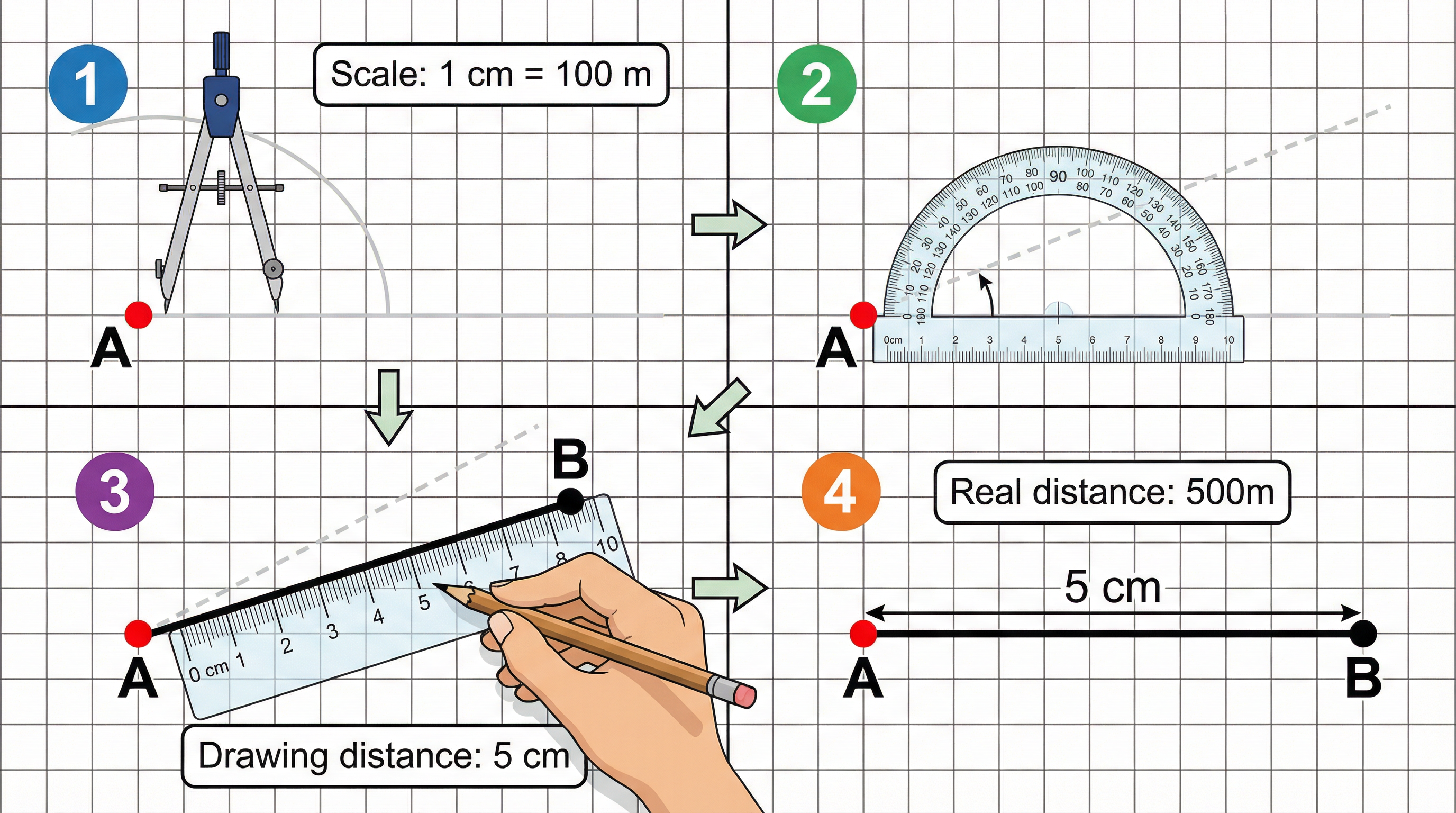
Example: A ship is 10 km from a lighthouse on a bearing of 110°. Using a scale of 1 cm represents 2 km, how would you draw its position? First, calculate the drawing distance: 10 km / 2 = 5 cm. From the lighthouse point on your map, draw a North line. Measure a 110° angle clockwise. Draw a line 5 cm long in this direction. The end of the line is the ship's position.

Mathematical/Scientific Relationships

The fundamental relationship in this topic is the formula that links the three key quantities:

Scale = Drawing Length : Actual LengthThis can be rearranged to solve for any of the variables:

• Actual Length = Drawing Length × Scale Factor (when using a 1:n ratio scale)
• Drawing Length = Actual Length / Scale Factor (when using a 1:n ratio scale)

**Unit Conversions (Must Memorise)**You must be fluent in converting between metric units. Mistakes here are common and costly.

• 1 kilometre (km) = 1,000 metres (m)
• 1 metre (m) = 100 centimetres (cm)
• 1 centimetre (cm) = 10 millimetres (mm)

Therefore, to convert from km to cm, you multiply by 100,000 (1000 × 100).

Practical Applications

Scale drawings are essential in many professions and everyday situations:

• Architecture and Construction: Architects create detailed floor plans and blueprints for buildings. Builders use these plans to construct the building accurately.
• Cartography (Map Making): Ordnance Survey maps use precise scales (like 1:25000 or 1:50000) to allow walkers, geographers, and the military to measure distances and navigate.
• Engineering: Engineers use scale drawings to design everything from bridges and cars to tiny electronic components.
• Interior Design: Designers use scale plans to arrange furniture in a room to ensure it fits and the space is used effectively.
• Gardening and Landscaping: A landscape gardener will draw a plan of a garden to scale to work out where to place paths, flowerbeds, and trees.